The Post-14 Mathematics Inquiry
Making Mathematics Count
The Report of Professor Adrian Smith's Inquiry into Post-14 Mathematics Education
Chapter 3 - Current Mathematics Pathways
-
The National Curriculum (pre-16)
- The curriculum post-16
- Mathematics qualifications: current progression routes within mathematics
- A summary of structures, qualifications and developments in Wales, Northern Ireland and Scotland
- The curriculum post-16
The National Curriculum (pre-16) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.1 | Progression through the school system in England and Wales is described in terms of four Key Stages: Key Stage 1 (pupils 5–7 years); Key Stage 2 (pupils 7–11 years); Key Stage 3 (pupils 11–14 years); Key Stage 4 (pupils 14–16 years). Although the focus of this Inquiry is post–14 mathematics education, in practice we cannot fully discuss post–14 pathways (Key Stage 4 and beyond) without a clear overview of mathematics pathways in Key Stages 1–3. Mathematics is a core subject of the National Curriculum (NC) in England and Wales throughout Key Stages 1–4. The expectation is that every student is taught some, or all, of the NC until aged 16. The NC was last revised in 1999, with the new curriculum in place from September 2000. Until 1999, England and Wales had a common curriculum in mathematics. Northern Ireland has always had its own curriculum and its own definition of key stages. The expectation is that every student is taught some, or all, of the Northern Ireland Curriculum (NIC) until age 16. The structure post–14 is essentially that of GCSE and GCE AS and A-level Mathematics, with some take up of Application of Number. Scotland has always had its own completely different structure. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.2 | Overwhelmingly, the concerns of respondents to the Inquiry have related to the English system. Unless otherwise stated, therefore, details in the text mainly refer to England. For completeness and comparison, detailed descriptions of the systems and recent developments in Wales, Northern Ireland and Scotland are provided at the end of this chapter. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.3 | The new curriculum for Wales is very similar to the previous joint curriculum for England and Wales, but in England the revisions to the mathematics curriculum were extensive. The content of the NC was not greatly changed, but the presentation of topics and the idea of progression was made much more explicit than before. These changes were made in response to widespread concerns about growing evidence of many pupils’ poor facility with the basic processes and calculations of mathematics, concerns which also led to the approval of adult numeracy and application of number qualifications for Key Stage 4 and older students. There was also concern that many pupils exhibited an inability to reason logically in mathematics, particularly in the areas of algebra and geometry. The curriculum changes were designed to help teachers emphasise important points in common areas of difficulty and misconception. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.4 | The full range of mathematics that should be taught in England at key stages 1, 2, 3 and 4 is set out in detail in the Programmes of Study (PoS) for Mathematics in the National Curriculum. All pupils are taught from a common curriculum to the end of Key Stage 3. There is a degree of differentiation at Key Stage 4 with two overlapping Programmes of Study called Key Stage 4 (Foundation) and Key Stage 4 (Higher). The PoS provide the basis for school planning and individual schools decide how to organise their school curriculum to include the programmes of study for mathematics. These decisions have been influenced in recent years by the impact of the National Numeracy Strategy and the Key Stage 3 Strategy, which have produced Frameworks for Teaching Mathematics for both the primary phase and for Key Stage 3, respectively. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.5 | The knowledge, skills and understanding sections in the PoS in England and Wales identify the main strands of mathematics in which pupils should make progress (Northern Ireland has its own PoS structure). The strands at each key stage are shown below. In Wales, an additional MA1 strand, Using and Applying Mathematics, is taught at each key stage. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.6 | Following the curriculum review in England in 1999, the Qualifications
and Curriculum Authority (QCA) has carried forward a major programme of proactive
development work in algebra and geometry with a view to producing guidance
to teachers of mathematics at Key Stages 3 and 4. This programme is also
intended to help inform future changes to the mathematics curriculum. The
PoS describe the intended content of the curriculum and the learning
opportunities that teachers should provide for all pupils. In addition, there
are four Attainment Targets, which set out expected standards of pupil’s
performance:
The Attainment Targets consist of eight level descriptions of increasing difficulty, plus a description for exceptional performance above level 8. Each level description indicates the types and ranges of performance that pupils working at that level should characteristically demonstrate. These level descriptions remained largely unchanged in the 1999 revision of the National Curriculum. The level descriptions provide the basis for making judgements about pupils’ performance in the National Tests at the end of key stages 1, 2 and 3. At Key Stage 1, it is expected that pupils will be working within the range of levels 1–3; in 2003, 90 per cent reached level 2 or above by age 7. At Key Stage 2, it is expected that pupils will be working within the range of levels 2–5; in 2003, 73 per cent reached level 4 or above by age 11. At Key Stage 3, it is expected that pupils will be working within the range of levels 3–7; in 2003, 70 per cent reached level 5 or above or above by age 14 and 49 per cent reached level 6 or above. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.7 | Evaluation of pupils at the end of Key Stage 4 (14–16) is normally through the externally assessed General Certificate of Secondary Education (GCSE) examination. GCSE assessment is the norm for all pupils who have achieved higher than NC level 3 by the end of Key Stage 3. Those who have not yet achieved at this level may take Entry Level qualifications, including, in England, the Certificate in Adult Numeracy. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.8 | GCSE and Entry Level qualifications are suites of qualifications within the National Qualifications Framework (NQF) for England, Wales and Northern Ireland. The NQF is managed jointly by three regulatory authorities – QCA for England, ACCAC for Wales and CCEA for Northern Ireland. These three regulatory authorities set the criteria for the development of specifications for GCSE Mathematics and Entry Level qualifications in mathematics. As we have indicated, Scotland has an altogether different structure. The GCSE examinations in England, Wales and Northern Ireland are administered by five awarding bodies, AQA, London Qualifications (Edexcel), OCR, the WJEC and the CCEA. Performance on GCSE Mathematics is determined, from the highest to the lowest grade, on an eight grade scale: A*, A, B, C, D, E, F and G. In the National Qualifications Framework (NQF), GCSE results grades A*– C are classified as a level 2 qualification, whereas grades D–G are classified as a level 1 qualification. GCSE therefore encompasses levels 1 and 2. Entry Level is below level 1. Level 3 mathematics qualifications are above the GCSE level 2 standard in terms of mathematics content and difficulty. Higher Education undergraduate degree courses are defined as level 4 and postgraduate courses as level 5. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
The curriculum post–16 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.9 | There is no statutory curriculum in England, Northern Ireland and Wales beyond the age of 16. Qualifications primarily for use post–16 are all externally assessed on a range of specifications developed to mathematics criteria set by the three regulatory authorities of England, Wales and Northern Ireland and all accredited by these authorities. Again, Scotland has a different structure. Significant changes to the curriculum and qualifications framework were made in the Curriculum 2000 reforms, which followed the extensive 1997 Qualifying for Success consultation with schools, colleges, universities and industry on proposals that were originally recommended in Lord Dearing’s Review of Qualifications for 16–19 Year Olds, published in 1996. At the time, there was a widespread consensus that change was required. The traditional programme of full-time study was increasingly seen as a less than adequate preparation for work or for the increasing number of generalist courses in Higher Education, which required a broader range of knowledge and skills than was hitherto the case. In addition, considerable concern was expressed – in particular, by the mathematics, physics and engineering communities – about the lack of mathematical fluency of those entering Higher Education courses requiring more specialist mathematics skills. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.10 | The five key elements of Curriculum 2000 were the introduction of:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.11 | There were five main principles underlying Curriculum 2000 reform:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Mathematics qualifications: current progression routes within mathematics |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.12 | At present, secondary mathematics qualifications split into two age-related
clusters: 14–16 qualifications (to the end of compulsory schooling)
and then 16–19 qualifications in the phase of post-compulsory schooling.
There are six main families of qualifications:
With the exception of Free Standing Mathematics Qualifications at levels 1 and 2, all the qualifications listed are approved and available for use pre–16 and post–16. FSMQ levels 1 and 2 are currently only approved for use post–16. In addition, there are mathematical units within a number of vocational qualifications. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.13 | Progression within mathematics is currently characterised by a potential chain of courses from the age of 14 onwards, students moving on from one level to take one or more qualifications in the next level up. Most students enter the chain from Key Stage 3 working mostly at level 1. Some aim to achieve a level 2 qualification in mathematics beyond the age of 16, having achieved a level 1 qualification by age 16. Others who have not achieved a level 1 qualification at age 16 try to reach level I by the age of 17 or 18. We shall discuss Free Standing Mathematics Qualifications (FSMQs) and AS Use of Mathematics in more detail later (paragraphs 3.32–38). Most students take these qualifications within the age ranges specified. A few may take GCSEs or GCEs at an earlier age than those specified. Some will take them at a later age than specified, and some will resit qualifications in an attempt to improve their grade. In the following sections, we provide a brief discussion of each available mathematics qualification. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.14 | The Inquiry has noted with considerable concern that very few students in England progress to level 3 qualifications in mathematics. A large proportion of the age cohort 16–19 in England choose programmes of study post–16 that do not include mathematics. The scale of the problem is typified by the progression rates of the cohort sitting GCSE in 2001: nearly 564,000 students (93 per cent of the age cohort) entered GCSE Mathematics, with nearly 51 per cent obtaining grades A* to C, and a 97 per cent overall pass rate; but in 2002, only just over 41,000 (6.5 per cent of the age cohort) entered for AS level. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GCSE Mathematics | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.15 | The GCSE was introduced in 1986 and the first examination was in 1988. It replaced the General Certificate of Education Ordinary Level (O-level) and the Certificate of Secondary Education (CSE), which had run in parallel. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.16 | Originally, GCSEs were graded from A–G. From 1994, the A* grade was introduced into the examinations to discriminate the very best performance. With one exception, all GCSE Mathematics specifications are now assessed through a combination of terminal examination and coursework. Northern Ireland’s GCSE in Additional Mathematics does not have coursework. The subject criteria for mathematics specify the balance between internal assessment (which must be externally moderated) and external assessment to be a ratio of 20:80. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.17 | GCSE Mathematics has had overlapping tiered papers since its first
examination in 1988. Pupils cannot be entered for more than one tier in any
given examination period. From 1998, most major entry subjects, with the
exception of mathematics, have been examined through a Higher Tier covering
grades A*–D and a Foundation Tier covering grades C–G. Mathematics
is the only subject to have retained more than two tiers. A small number
of subjects, including art, music, PE, and history, have one tier. The intent
of the three-tiered papers in mathematics was to cover a range of GCSE grades,
so that candidates can attempt questions that are matched to their broad
ability and enable them to demonstrate positive achievement.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.18 | Schools base their decision on which tier to enter pupils for on their Key Stage 3 results and on their expected level of achievement in the examination. In the revised National Curriculum, there are two underpinning PoS at Key Stage 4: Key Stage 4 (Foundation) and Key Stage 4 (Higher). At present, this two-tier structure of the curriculum in England is not mirrored in the structure of GCSE assessment. The Foundation PoS is the appropriate course for those pupils who expect to achieve up to grade C standard GCSE Mathematics, but not beyond. The appropriate grounding needed for progression to GCE AS and A level is only covered in the Higher PoS at Key Stage 4. This includes more abstract and formal mathematics than does the Foundation POS, which has more emphasis on everyday and more practical examples. The revised curriculum recommends that all pupils who have obtained a good level 5 or better in mathematics at the end of Key Stage 3 should be taught the Higher Key Stage 4 PoS for mathematics. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.19 | Table 3.1 shows the numbers entered for GCSE Mathematics in England for each of the years 1999–2003, together with the percentage of the age cohort entered and the percentage of the age cohort attaining grades A*–C. For example; in 2003, 585,000 students out of a total cohort of 622,165 were entered for GCSE Mathematics (94 per cent) and 298,600 (48 per cent of the age cohort, 51 per cent of those entered) attained grades A*–C. A total of 562,000 attained grades A*–G (96 per cent of those entered). The percentage of those entered obtaining a pass grade has remained stable at around 96 per cent for the past few years. The percentage of those entered attaining grades A*–C has moved from just below to just above 50 per cent over the five-year period. The total percentage of the age cohort entered has increased slightly over the past decade from about 95 per cent to 97 per cent. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
GCE AS and A-level Mathematics and Further Mathematics |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.20 | General Certificates of Education (GCEs) are single subject qualifications. They were restructured for first teaching from September 2000 in response to decisions taken in April 1998 following the Qualifying for Success consultation. These revised GCEs are part of the Curriculum 2000 reforms. GCE AS and Alevel specifications are based on rules set out in the regulatory authorities’ Common, GCE and subject criteria. The latter may specify some of the required content. In the case of GCE mathematics, this core of pure mathematics occupies 50 per cent of current specifications. All GCEs in Mathematics also contain at least 25 per cent of mechanics, statistics or discrete mathematics, or some combination of these applications. There are, nonetheless, significant differences in both the detailed structure and content of specifications offered by individual awarding bodies or across awarding bodies, and in the style of their examination questions, to provide an element of choice for centres. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.21 | Mathematics is unique at GCE level since candidates can obtain more than one A-level’s worth of the subject. There are also qualifications in GCE AS and A-level Further Mathematics. These take the subject further than the study of GCE A-level Mathematics alone. Assuming that teaching resources are available, very able students will often be entered for both A-level Mathematics and A-level Further Mathematics. Some may even study and be examined in more than 12 modules, and so gain more than the equivalent of two full A-levels in Mathematics (which each correspond to 6 modules). In recent years, secondary schools have accounted for just below 70 per cent of A-level entrants in Mathematics, with Sixth Form Colleges providing just under 20 per cent and the rest being entered from FE/Tertiary Colleges. For AS levels, secondary schools are providing over 75 per cent of entrants, Sixth Form Colleges around 15 per cent and the rest are being entered from FE/Tertiary Colleges (JCGQ Inter-board Statistics). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.22 | Lord Dearing’s review of 16–19 qualifications contained many references to qualifications in pre–16 mathematics, GCE Mathematics and Further Mathematics. Many of the key features of his remarks and recommendations for GCSE and GCE Mathematics, and about bridging the gap between them, were built into the 1999 National Curriculum review to age 16 and the Curriculum 2000 reforms for the post–16 age group. The Curriculum 2000 reformed GCE A-levels are modular with examinations that can be taken at various stages during, or at the end of, a two-year course. The qualification is designed in two parts. A first half – the GCE Advanced Subsidiary (AS) – that assesses the knowledge, understanding and skills expected of candidates half way through the course; followed by a second half (A2). AS and A2 together are intended to maintain the standard of the full A-level qualification prior to Curriculum 2000. The AS may be taken as part of the whole A-level or as a free-standing qualification. The full A-level normally comprises six modules, three each in the AS and A2 stages. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.23 | During 2000/01, serious difficulties with AS Mathematics were reported to the regulatory authorities. The overriding concern of teachers was that AS Mathematics appeared to be too difficult and was turning many students away from the subject. The results of the first cohort of candidates appeared to confirm this. The pass rate among the 17 year-old cohort was 71.8 per cent, very low compared to other mainstream subjects like English, history, geography, physics, chemistry and biology. Although in subsequent years, the AS pass rate in Mathematics had increased, it still remains conspicuously out of line with other mainstream subjects. Table 3.2 presents comparative figures for 2001–03. The Inquiry note with concern this considerable disparity and, in relation to student choice of subjects post–16, the perception problem this presents for the discipline of mathematics and the subsequent supply chain for mathematics, science and engineering. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.24 | Detailed analysis of the AS Mathematics syllabus and assessment undertaken by the regulatory authorities in Autumn 2001 showed that in terms of both the specifications for AS and their associated examination papers the amount of content and the demand of the new papers was prima facie no greater than before. However, it was clear that what had worked well prior to Curriculum 2000 no longer worked. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.25 | With a 3 + 3 split of core pure mathematics plus applications for the full Alevel, it was impossible for those teaching the material not to include some core A2 material in the AS. Retrospectively, it was therefore recognised that the content of the AS specifications was too great to be taught and mastered by students in the time available before May/June of their first year of post–16 study. There appears now to be an acceptance that students need time to mature into a two-year advanced course, and that learning is faster and material becomes more established in the second year of the course. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.26 | Whilst work was underway to revise the GCE Mathematics criteria, the
regulatory authorities and the three administrations in England, Wales and
Northern Ireland agreed that no changes could be implemented until an entire
GCE cycle was completed and analysed. When the full Curriculum 2000 A-level
was examined for the first time, and the AS had been through its second round,
the 2002 summer results showed that:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.27 | Faced with these serious declines in take up of AS and A-level Mathematics
and Further Mathematics following the Curriculum 2000 reforms, the decision
was made to proceed with the development of new specifications to the revised
criteria for GCE Mathematics. These had been developed during the year by
QCA, ACCAC and CCEA in conjunction with an expert panel of stakeholders.
The revised criteria have now been approved. They retain the existing core
content, but now spread over four units instead of three (2 AS and 2 A2).
This means that:
The revised specifications have been available from autumn 2003, taught from September 2004, with first AS examinations in 2005 and first A2 examinations in 2006. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.28 | All GCE AS and A levels are certificated on a scale A to E, with U (unclassified) and X denoting a fail. A previous grade N, denoting a narrow failure, was discontinued after 2001. The breakdowns of grades awarded for A-level and AS level Mathematics for the past four years (A-level) and three years (AS level) are shown in Tables 3.6 and 3.7, respectively. The Inquiry has noted with interest the fact that the distributions of grades for mathematics do not follow the bell-shaped curve typically observed in many other subjects. Instead, grade A is the most commonly obtained grade. We shall comment further on this in paragraph 4.37. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Advanced Extension Award (AEA) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.29 | As part of the Curriculum 2000 reforms, Advanced Extension Awards (AEAs) were introduced for advanced level students in England, Wales and Northern Ireland to provide challenge for the most talented students. AEAs, for which the first examination was in summer 2002, are externally assessed through written examination. They are awarded at merit and distinction grades and supersede what were previously called Special Papers. The AEA in Mathematics was developed and trialled from 2000 to 2001 and is assessed by a single three-hour paper. All questions are based on the common core of pure mathematics from the A-level mathematics subject criteria. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.30 | In 2002, nearly 40 per cent of the candidates for A-level Mathematics
obtained a grade A result. The AEA in Mathematics is aimed at the top 10
per cent of the A-level Mathematics candidates nationally, ie. the top one
third of the potential grade A cohort. It aims to enable students to:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.31 | Questions on the AEA paper are much longer and less structured than those in the modular papers. They require a greater level of understanding than for GCE A-level as well as the ability to think critically at a higher level. The AEA is not expected to require the teaching of additional content, but requires exposure to deeper forms of reasoning and rigour, and a less compartmentalised approach to problem solving. Students are awarded additional marks for their ability to develop creative, and perhaps unexpected, solutions to problems. The AEA has proved more accessible than the Special Paper it replaced. The initial take up of the AEA in Mathematics has been encouraging, with approximately 1000 candidates in each of the two sessions to date. Provisional data a combined merit and distinction pass rate of 32 per cent in 2002 and 42 per cent in 2003. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Free-standing Mathematics Qualifications (FSMQs) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.32 | In view of the widespread concerns expressed to us about current
post–16 provision, the Inquiry has been particularly interested in the
recent development of Free Standing Mathematics Qualifications, which were
developed by the QCA as a specific response to perceptions of serious gaps
in mathematics provision post–16. Important target groups that were
felt to be overlooked included:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.33 | FSMQs were developed at each of levels 1–3. The units were intended to meet individual student need at a level suited to the student’s current level of mathematical understanding. Each unit is completely self-contained and students are directed to titles that complement their other study programmes. The level 1 FSMQs are designed for students on vocational courses, including some of those pursuing level 3 qualifications, who do not possess a level 1 qualification in mathematics including a GCSE grade D–G. The level 2 FSMQ qualifications are designed for those who have achieved GCSE at Foundation Tier and want to aspire to some mathematics at level 2, but wish to follow a route different from the GCSE route. The level 3 qualifications are designed for those wanting some form of focused mathematical study beyond the upper end of GCSE. In size terms, each unit was conceived as 60 hours of teacher contact time. FSMQs are intended to provide a different approach to studying and learning mathematics, designed to fit into the individual student’s study programme. They aim to increase mathematical competence and develop transferable mathematical skills by using mathematics in a range of contexts. The use of ICT is integral to the units and real data is used wherever possible. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.34 | As an integral part of the learning and assessment process, students produce a portfolio of mathematics work, applying mathematics in contexts familiar from their study programme, work or leisure interests. This is intended to give the mathematics an immediate relevance and help motivate students to learn. In addition, FSMQs aim to test process skills more than just content knowledge. Students are encouraged to think about mathematics and present clear arguments in their work. They are also encouraged to read mathematical scenarios, presented in a variety of styles. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.35 12 FSMQs were developed from 1997 and piloted from
1998–2000; 11 of these became nationally available qualifications from
2001. The original set of eleven FSMQs are:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.36 | Most of the units deal with generic topics and skills, although some of them are clearly aimed at specific knowledge and skills needs. For example: Making connections in mathematics is designed for students who may apply for primary Initial Teacher Training; Using and applying statistics supports, in particular, teaching in A-level Psychology or in A-level Geography; Managing money and calculating finances support vocational business studies courses. The original units are all assessed through 50 per cent portfolio and 50 per cent written examination, both assessed externally. FSMQs are graded A–E: A being the highest pass grade and E the lowest. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.37 | Two further FSMQs have been accredited recently, which differ in format from the earlier set. Foundations of advanced mathematics is a level 2 qualification designed to bridge intermediate GCSE Mathematics and AS Mathematics. Additional mathematics is a level 3 mathematics qualification, not involving portfolio component, designed for year 11 students who gain GCSE Mathematics with high grades in year 10 and want to continue mathematics whilst doing other GCSEs in year 11. Northern Ireland has the distinctive feature of a GCSE in Additional Mathematics, which is a level 2 rather than a level 3 award, even though its content goes beyond the Key Stage 4 Programme of Study. (see, also, paragraph 3.63). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.38 | The Inquiry notes that since 2001 the number of candidates taking FSMQs has grown substantially, from around 2000 in 2001, to around 4,500 in 2002, to just over 6000 in 2003. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
AS – Use of Mathematics |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.39 | The AS Use of Mathematics qualification was introduced in September 2001.
This qualification is designed for students who achieve at least GCSE Grade
C at the end of compulsory schooling and who wish to continue with a general
mathematics course post–16 without taking a full A-level. It focuses
on developing process skills of application, understanding, reasoning,
explanation and communication of mathematics. Currently, this qualification
is only available at AS level. AS Use of Mathematics has three components
(where (*) indicates that the component is a level 3 FSMQ): two are mandatory
units, Working with algebraic and graphical techniques (*) and
Applying mathematics (the terminal unit); for the remaining component,
there is a choice between Modelling with calculus (*) and Using
and applying statistics (*). The AS Use of Mathematics aims to develop:
Learning is assessed through written examination and a coursework portfolio, with the terminal unit wholly assessed through written examination. This differs from the assessment of AS Mathematics in that the weighting of student portfolio work to external written examination is 1:2. AS Use of Mathematics is the only full proxy for level 3 Application of Number. In 2003, there were just over 500 entries for this qualification. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Key Skills Qualifications in Application of Number |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.40 | Application of Number qualifications, as part of the key skills portfolio, are available at levels 1–4 in England, Wales and Northern Ireland. In recent years, there has been a clearly expressed view from employers and others that GCSEs often do not equip learners with useful number skills, or the ability to use number in the contexts of other subjects, or the workplace. The call from employers and others has been for individuals to be enabled to acquire applied, transferable number skills, which will support them in work and beyond. These views have informed the design of the Application of Number qualifications and the development of keys skills teaching and learning approaches. The Inquiry has noted that in response to these views the development of the Application of Number strand has taken place completely separately from the development of mathematics provision for GCSE and AS/A–levels. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.41 | Current Government policy in England identifies key skills as a range of essential generic skills that underpin success in education, employment, lifelong learning and personal development. The recent DfES publication 14–19: opportunity and excellence – volume 1, (DfES 0744/2002) included the following statement (paragraph 3.8): “To help ensure that all young people are well equipped in literacy, numeracy and computer skills we will introduce an entitlement for them to continue studying up to age 19 until they reach the standard of a good GCSE or the corresponding level 2 key skill qualification. Those going on to higher education or professional study after 19 should be encouraged to achieve a level 3 qualification in at least one of these skill areas.” This expectation in England is supported by the LSC entitlement funding for fulltime learners in schools and colleges. In work-based training, level 1 achievement in number (and communication) is the minimum requirement for Foundation Modern Apprenticeships (FMA). The requirement for Advanced Modern Apprenticeships (AMA) is achievement at level 2. The Skills White Paper (paragraph 5.27e) announced that a level playing field in basic and key skills funding would be established between the work-based and full-time FE routes from 2004/05 onwards (although, of course, the work-based route still relies on employers being willing to release students for appropriate study periods). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.42 | National standards for the suite of six key skills (then titled “core skills”) were initially developed in the early 1990s, following joint work by the National Council for Vocational Qualifications and the Schools Examination and Assessment Council. The national key skills canon comprises: Application of Number, Communication, Improving Own Learning and Performance, Information Technology, Problem Solving, Working with Others. Their development represented a response to the nationally recognised need for applied and transferable skills in the global labour market of the late 20th century, and the case for a common core or entitlement curriculum post–16. They formed an explicit component of GNVQs (introduced in 1992) and of Modern Apprenticeship frameworks (introduced in 1995). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.43 | Prior to the introduction of Curriculum 2000, the Application of Number, Communication and IT key skills qualifications were only available through Advanced and Intermediate GNVQs, assessed solely through an externally verified/moderated portfolio of coursework evidence. Candidates had to show that they could apply the skills in a range of contextual and practical situations. With the introduction of Curriculum 2000, a short external test was added to this portfolio component with the intention of providing corroboration that candidates had genuinely achieved the underpinning skills. There is no compensation between the two assessment components: candidates have to pass each component separately to pass the qualification. There are no grades other than pass or fail. Following the implementation of the Curriculum 2000 reforms, the provision and acquisition of revised key skills qualifications for all students became a central goal of Government policy in the training and development of a numerate, literate and ICT skilled workforce for a modern economy. Funding incentives were provided to schools, colleges and other training institutions to promote key skills and achievement for all post–16 year olds, in line with Government policy. As recommended in the Cassels Review, all Modern Apprenticeship frameworks require achievement in communication and number skills, through good GCSEs or the corresponding key skills qualifications. Additional key skills requirements are included in frameworks at the discretion of the responsible sector body. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.44 | The key skills standards are centrally developed by the QCA, CCEA and ACCAC and offered as qualifications by 18 awarding bodies (representing the wide variety of candidates that need to acquire key skills). Student portfolios have to reflect accurately the specific requirements of each specification. The key skills qualifications in Application of Number, like those in Communication and IT, are free-standing qualifications formally available at levels 1–4 of the NQF. They are intended to serve a number of target audiences: eg those with good GCSEs who need or wish to develop their applied number skills further post–16, through the level 3 and 4 qualifications, without specialising in mathematics; those who have secured less good grades at GCSE and need or wish to achieve a level 2 qualification in number skills post–16; those who wish to progress from basic numeracy skills, developed through Entry level qualifications or the national numeracy tests. The Application of Number external tests at levels 1 and 2 serve also as the sole tests for Adult Basic Numeracy qualifications at these same levels. All publicly funded qualifications in adult basic numeracy are based on the national standards set by the regulatory authorities. Entry Level achievement can be certificated at each of the three sub divisions of Entry Level. For Entry Level qualifications, external assessment contributes a minimum of 50% to the overall award, but at levels 1 and 2, assessment is entirely by the external AoN tests at these levels. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.45 | Proxy qualifications are those qualifications that have been agreed by the regulatory authorities to assess the same knowledge and skills as aspects of the key skills qualifications. Candidates can claim exemption from all or part of particular key skills qualifications for up to three years from the date of the award of the specific accredited proxy qualification. GCSE mathematics at grades A*–C acts as a proxy for the external test of AoN at level 2 and a pass in AS or A-level Mathematics acts as a proxy for the external test of AoN at level 3. AS Use of Mathematics, comprising two of the FSMQ units together with one unit unique to the qualification, acts as a full proxy for both the portfolio work and the external test of AoN at level 3. All nationally accredited qualifications (including GCSE and GCE) are required to signpost opportunities for the learning and demonstration of key skills, including Application of Number. As result of the Skills White Paper in England, QCA have asked awarding bodies to improve their guidance in this area. For example, each FSMQ has a detailed map showing exactly how that qualification contributes to AoN portfolio assessment. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.46 | Students on many level 3 courses are awarded UCAS points for all level 3 qualifications that they pass. Each of the key skills qualifications at level 3 carries a UCAS tariff of 20 points; however, level 3 students also can be awarded a key skill at level 2 and for each of these they are awarded 10 UCAS points. This is the only instance where a level 2 qualification is awarded UCAS points. Thus, for example, a student who is awarded Communication and IT key skills qualifications at level 3 and AoN at level 2 will be awarded 50 UCAS points; a student with all three key skills at level 3 will be awarded 60 UCAS points, the same tariff award as an A grade for GCE AS Mathematics. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.47 | The external tests for AoN at levels 1 and 2 are available monthly, on-demand (weekly or higher frequency) and, via selected awarding bodies, on-line. Calculators are not allowed in these tests. The format of the tests is multiplechoice and lasts for 11/4 hours. Teachers may at their own discretion extend the duration of the test by as much as 25 per cent if they feel that their candidates need extra time. The level 3 test of AoN is available six times a year. It is a free response and calculator allowed test with six or seven multipart questions. This test lasts 2 hours. The pass mark for each test is set jointly by the awarding bodies. Work is nearing completion on preset pass marks, which will further support the current high frequency testing opportunities and speed learner feedback. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.48 | The Statistical First Release covering the period between October 2000 and September 2002 showed that 296,000 key skills qualifications had been awarded to 206,300 candidates. Of all the key skills qualifications awarded in that period, 60 per cent of awards were obtained in FE/Tertiary Colleges, 20 per cent in secondary schools and 12 per cent in Sixth Form Colleges; 90 per cent of awards were to those aged 19 and under. We also note that 46 per cent of qualifications were obtained at level 2, 37 per cent at level 1 and 17 per cent at levels 3 and above. The majority were awarded in England (88 per cent), with 8 per cent awarded in Wales and 3 per cent in Northern Ireland. Of the 296,000 qualifications awarded, 25 per cent were for Application of Number compared with 39 per cent for Communication and 36 per cent for IT. A greater proportion of candidates gaining awards in Application of Number gained their highest qualification at level 1 compared to those only gaining level 1 in the other qualifications (46 per cent compared to 31 per cent in Communication and 38 per cent in IT). A review of the key skills specifications by the regulatory authorities reported to ministers in December 2003. The revised specifications for Application of Number and other key skills are due to take effect from September 2004. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Adult basic numeracy |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.49 | Skills for Life, the national strategy for improving adult literacy and numeracy skills in England was launched by the Government in March, 2001, and aims to improve the basic skills of 750,000 adults by 2004 and 1.5 million adults by 2007. The all-age National Basic Skills Strategy for Wales was launched in 2001. It is estimated that 7 million adults (1 in 5) in England cannot read or write at the level expected of an average 11–year-old. It is estimated that even more (perhaps 1 in 4 adults) have problems with numbers. Labour market studies show that having level 1 numeracy skills are associated with having up to a 4 percentage point higher likelihood of being in employment than someone without level 1 skills, and that an individual with at least level 1 numeracy skills will earn on average between 6–10 per cent more than an individual with numeracy skills below level 1. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.50 | The provision of mathematics education for adults up to level 2 has been
a key component of the Skills for Life strategy. The LSC makes numeracy provision
available free to all adults irrespective of their starting point, geographical
location or learning context or setting.The strategy sets out four strands
to address numeracy deficiencies:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.51 | The new Adult Numeracy qualifications, which are part of the strategy, are available at three stages of Entry level and levels 1 and 2, while AoN key skills qualifications start at level 1. The Adult Numeracy qualifications at levels 1 and 2 are only available by taking the same external tests as those for AoN at levels 1 and 2, respectively. In contrast, the Adult Numeracy Entry Level qualifications have more flexible assessment procedures, offering a range of options for different types of learners. In general, the recent unification of the different examinations in adult numeracy seems to have been welcomed. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.52 | LSC actions so far to secure improvements in adult numeracy skills in
England include:
Family programmes can also play a significant role in improving adult numeracy skills and in fostering greater involvement between children, their parents and their communities. The Adult Basic Skills Strategy Unit (ABBSU) is working with the LSC, who now fund family programmes, to expand and extend family literacy, language and numeracy provision. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.53 | In addition to the role of ICT in assessment, work has been done with Ufi/learndirect to support the development of both literacy and numeracy skills through e-learning. Evaluation of the experiences of adult learners who have participated in these programmes shows that 92% find the use of ICT motivating and most feel that ICT enables them to produce a higher standard of work more quickly. 64 per cent of learners said that ICT helped them to learn and in particular to concentrate. The ABBSU is continuing to work with other agencies to develop and disseminate e-learning methods and resources to support the development of a range of skills including numeracy. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
A summary of structures, qualifications and developments in Wales, Northern Ireland and Scotland |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
WALES |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lower secondary – age 11–16Assessment at Key Stage 3 (age 11–14) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.54 | The main aspects of the National Curriculum at Key Stages 3 and 4, the means of assessment, the structure of the National Curriculum attainment targets, the attainment level descriptions and the expectations for attainment by the end of Key Stage 3 are the same in Wales as in England. In the 2002 Key Stage tests, 62 per cent of pupils achieved level 5, or above, in mathematics. In Wales, the tests, together with guidance on their use and mark schemes are produced by the Qualifications, Curriculum and Assessment Authority for Wales (ACCAC), which is also responsible for evaluating the effectiveness of the assessment arrangements. The tests are marked by external markers appointed by an external marking agency. ACCAC has also developed the optional assessment materials (OAMs) to support teacher assessment in selected subjects at any point during Key Stage 3. The aim of OAMs is to lead to greater coherence in teacher assessment and provide comparable information about pupils’ progress. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Assessment at Key Stage 4 (14–16) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.55 | The assessment arrangements in Wales are currently the same as those in England, but we have noted that the Interim Report of the Daugherty Assessment Review Group envisages different arrangements for assessment of 11–14 year olds in the future. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Assessment 16–19 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.56 | The arrangements in Wales are currently the same as those in England. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Developments |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.57 | In October 2002, the Welsh Assembly Government published Learning Country: Learning Pathways 14–19, which set out proposals for 14–19 learning. This was followed by the publication of the Action Plan on 2 April 2003. One of the key proposals is that, subject to the outcome of piloting, the Welsh Baccalaureate, which has been in pilot post–16 since September, 2003, should become a national award at Foundation, Intermediate and Advanced levels from September 2007. Initially the Welsh Baccalaureate is being offered post–16 at levels 2 (Intermediate) and 3 (Advanced) of the NQF. It is being piloted with three cohorts beginning in successive years (2003, 2004 and 2005). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.58 | The Welsh Baccalaureate contains three elements: a common Core curriculum, with a notional time allocation of 4.5 to 5 hours per week, comprising the six key skills, Wales, Europe and the World (including language modules), Work-related Education (including work experience and entrepreneurship) and Personal and Social Education (including an element of community participation); Optional studies, with an allocation of 18 to 20 hours per week, comprising the main programme of learning selected from existing courses leading to qualifications in the NQF (eg GCSE, GCE, NVQ); and the tutoring/mentoring system that links programme and student. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.59 | The Intermediate Welsh Baccalaureate will require all students to complete the three core key skills (AoN, Communication and IT) and two of the other three wider key skills (Improving one’s own learning and performance, Problem-solving and Working with others, although these have not yet been accredited to the NQF) at level 2 and obtain 5 GCSE grades A*–C, or the equivalent. For the Advanced Welsh Baccalaureate, the student must attain three key skills (including at least one of the core three) at level 3 and the other three at level 2 and 2 GCE A levels grades A–E or the equivalent. This means that all those aspiring to the Intermediate Welsh Baccalaureate will need to have achieved Application of Number at level 2 and all Advanced Baccalaureate students will need to have achieved it at either level 2 or 3. Students will also be able to choose mathematics qualifications at the appropriate levels as part of the ‘options’ component of their programme. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.60 | The Credit and Qualifications Framework (CFQW), which will offer credit for qualifications in the NQF, will continue to be developed with a view to progressive rollout from May 2003 until 2006 when the essential building blocks are expected to be in place. It will be extended to reflect achievement through prior and informal learning and of voluntary qualifications. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
NORTHERN IRELAND Post Primary – 11–16 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.61 | The broad structure for the delivery of a statutory curriculum and assessment
arrangements for 11–16 year olds is similar to those in England and
Wales with some differences. We note, however, that schooling in Northern
Ireland starts at the age of 4, with children completing 7 years in primary
before transferring to post primary at the age of 11. Key Stages and years
do not therefore match those for England. In the Northern Ireland system:
KS1 is ages 4–8 and years 1–4; KS2 is ages 8–11 and years
5–7; KS3 is ages 11–14 and years 8–10; KS4 is ages 14–16
and years 11–12. The main strands of mathematics in which pupils should
progress at each key stage are set out below:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Assessment at Key Stage 3 (11–14) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.62 | At Key Stage 3, statutory assessment of English, Irish (in Irish speaking schools), mathematics and science takes the form of teacher assessment (without moderation) and the end of key stage subject tests with parallel reporting of both the teacher assessment and test outcomes. For mathematics, for most tiers of entry, there are two written papers and a mental mathematics test. The written tests, each lasting an hour, are based on the related POS and address all the attainment targets except Processes in Maths. There are five tiers, covering Northern Ireland Curriculum levels 3–8, with five written papers of which two are used for each tier except tier A and two mental tests, 1 and 2 (ie: Tier A, written paper 1 only, plus mental test 1; Tier B, written papers 1 and 2, plus mental test 1; Tier C, written papers 2 and 3, plus mental test 2; Tier D, written papers 3 and 4, plus mental test 2; Tier E, written papers 4 and 5, plus mental test 2). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Assessment at Key Stage 4 (14–16) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.63 | Revised GCSE specifications, including those for mathematics, were examined for the first time in summer 2003. Northern Ireland has the distinctive feature of a GCSE in Additional Mathematics, which is a level 2 rather than a level 3 award, even though its content goes beyond the Key Stage 4 Programme of Study. This is unusual in having no coursework element and is accredited by the QCA for use in Northern Ireland only. The take up is mainly from stronger GCSE candidates, who sit the examinations in year 12 (corresponding to year 11 in England), sometimes in tandem with standard GCSE Mathematics, sometimes having taken the latter the year before. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Assessment 16–18 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.64 | Northern Ireland implemented the Curriculum 2000 reforms alongside England and Wales. The CCEA worked with the other regulatory authorities to revise the mathematics specifications in response to early evaluations that indicated that the overall content of the AS Mathematics was too great. Northern Ireland will also introduce the revised specifications for first teaching from September 2004. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Examination Arrangements |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.65 | The CCEA is both an awarding body providing, among others, GCSE, GCE and key skills qualifications and one of the regulatory authorities responsible for ensuring the continued availability of high quality qualifications that are fit for purpose, command public confidence and are understood both by those who take qualifications and those who use them. In order to ensure that a consistent and uniform approach is taken to regulation, it works closely with ACCAC and QCA. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Developments |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.66 | A fundamental review of the Northern Ireland curriculum has been completed by CCEA. Proposals would limit the role of statute to specifying only the minimum entitlement of every pupil. At Key Stage 3, the statutory curriculum would be specified in terms of: curriculum areas and not individual subjects (although mathematics remains an area in its own right); and a common minimum entitlement for every pupil, irrespective of future intentions. Schools would have the flexibility to extend this entitlement to cater for the needs of different pupils. At Key Stage 4, the proposals would mean a statutory curriculum limited to: Skills and Capabilities (including Communication, Using Mathematics, ICT, Problem-solving, Self Management and Working with Others); Learning for Life and Work (including PSHE, citizenship and education for employability); and Physical Education. There would be no requirement in law for pupils to study any individual subject, but it would be expected that for most pupils their programme at Key Stage 4 would continue to consist of a range of GCSE courses, or courses leading to other appropriate qualifications and that a course in mathematics would be amongst these. Indeed it is proposed that all qualifications in mathematics offered to pupils in Key Stage 4 in Northern Ireland should provide all the learning opportunities identified for Using Mathematics and therefore that the accreditation criteria should be altered accordingly. Once these provisions are in place it will be necessary to change the specifications for mathematics accordingly. This will have the effect of making it no longer necessary for pupils to undertake additional qualifications such as Key Skills in order to demonstrate competence in Using Mathematics. (Similar arrangements will pertain to Communication and English). If accepted, it is likely that phased implementation of these changes will commence in September 2005. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.67 | The review of the statutory curriculum has been accompanied by a review of the statutory assessment arrangements associated with it. CCEA recommends that the current tests in English, mathematics and science for 14–year olds be discontinued. End of key stage tests would be replaced by a system of standardised annual reports. If the proposals are accepted, CCEA will work with schools to explore more collaborative approaches to the curriculum beginning with Key Stage 3 and possibly extending into Key Stage 4. Each “subject” will be asked to make relevant links to other areas. In this scenario the nature of the mathematics being learned could then be applied to different scenarios across the curriculum. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.68 | Arrangements are being put in place for a single managed service entitled ‘Learning Northern Ireland (LNI)’ covering all aspects of the use of ICT in schools both for administrative and curricular purposes. One of the items of work which may contribute to this in the future is a project in computerbased formative assessment, partly in the area of mathematics. In this project a facility has been developed that allows for the playback of stages of a pupil’s work in a way that will help the pupil appreciate the processes involved. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Scotland |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.69 | There is no statutory national curriculum in Scotland. However, guidance is provided by the Scottish Executive Education Department and other national agencies. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Structure of school education |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.70 | School curricula are divided into two phases: 5–14 and National Qualifications. Following transfer from primary to secondary (at the end of year 7), the various Scottish Qualifications Authority (SQA) examinations have traditionally been taken at possible exit points from the school system. These are: Standard Grade at the end of S4 (year 11), Access, Intermediate 1, Intermediate 2 or Highers at the end of S5 (year 12), and additional Access, Intermediate 1 or 2, Highers or Advanced Highers (AH) in S6 (year 13). These arrangements are reflected in Age and Stage Regulations, which determine the age at which students may be assessed and receive external certification for the National Units and Courses managed by the SQA. However, schools and other centres, if they wish, also apply to the SQA for exceptional entry in order to present the most able students for examination at an earlier age. These arrangements have and are being revised to introduce more flexibility within the education system. National Qualifications (NQs) now incorporate Standard Grades and new National Qualifications (Access, Intermediate, Intermediate 2, Higher and Advanced Higher), which were introduced through the “Higher Still” reforms. The Scottish Executive’s response to the National Debate on Education (see paragraph 3.83) also contains the commitment to consult on the future of Age and Stage regulations. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.71 | National guidelines for the 5–14 curriculum and course arrangements for Standard Grade and new National Qualifications give guidance on course content. The new NQ courses offer a measure of choice at each level, although all courses are based on generic maths until more advanced levels (Higher and Advanced Higher) where specialisation is possible. University entrance requirements are normally framed in terms of Higher awards and it is common for school students during year S6 to gain unconditional entry to universities on the basis of the Higher awards achieved in S5. Other students will, during year S6, receive conditional entry to Higher Education. Conditions usually refer to outstanding Higher awards but also sometimes refer to Advanced Higher targets. Both schools and colleges may deliver new National Qualifications at levels ranging from Access 1 to Advanced Higher. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Scottish Credit and Qualifications Framework |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.72 | The Scottish Credit and Qualifications Framework (SCQF) provides a structure
that helps to relate qualifications at different levels ranging from Access
to Postgraduate levels. In these ways it assists learners to plan their progress
and to minimise duplication of learning. The SCQF provides a national vocabulary
for:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
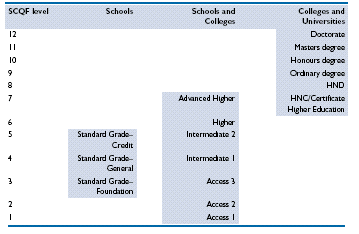
| 3.73 | In the SCQF, there are 12 levels ranging from Access level 1 (designed
for learners with severe and profound learning difficulties) to level 12
(associated with postgraduate doctoral studies). The awards and their
relationship to SCQF levels are illustrated in the table.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Assessment 14–16 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.74 | Most pupils aged 14–16 (S3 and S4) will take a range of Standard Grade courses. National guidance recommends that mathematics is one of the courses that pupils study. Each Standard Grade course lasts two years and is generally taken at the end of S4 (year 11). It has two or three assessable elements. Assessments can take the form of an examination, coursework or performance. The mark for each element is aggregated to give the overall grade. Mathematics has two assessable elements: Knowledge and Understanding and Reasoning and Enquiry. Both elements are externally assessed by the SQA through an examination. Awards at Standard Grade are set at three levels: Credit (grades 1–2), General (grades 3–4) and Foundation (grades 5–6). Credit is the highest level of achievement | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Assessment 16–18 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
“Higher Still” reforms |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.75 | New National Qualifications were introduced as a result of the “Higher
Still” development programme. They are intended to provide a coherent,
progressive educational experience for all students within post–16
education. Pupils aged 16–18 (S5 and S6) take a range of National
Qualifications courses. The number and subjects to be studied are agreed
through a guided process of negotiation between pupil and school to ensure
an appropriate curriculum. National Qualifications courses are offered at
five levels:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.76 | Advanced Higher is the highest level of achievement and normally studied in S6. Each course lasts one year although, as courses are unit-based, a longer period of study is possible. Almost all courses at Intermediate 1, Intermediate 2, Higher and Advanced Higher levels consist of 3 units. An internal assessment is carried out at the end of each unit (known as a National Unit). Each unit counts as a qualification in its own right. Pupils must pass internal assessments in all the relevant units and then, separately, an external assessment to attain an overall course award. The external assessment, carried out by SQA, determines the grade (A–C) of the course award. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.77 | National Qualifications courses in mathematics cover a range of knowledge, skills and understanding appropriate to each level of course. Topics include problem solving, applied mathematics and algorithms. For mathematics at Intermediate 1 and 2, students have a choice of the third unit of the course. The normal unit 3 is designed to allow progression to the next level (so, for example, a student with units 1, 2, 3 at Intermediate1 could go on to take Intermediate 2 the following year). Instead of unit 3, the student can take an applications unit that gives opportunities to apply what has been studied in suitable contexts and undertake a short project – but this unit does not articulate with the next level. Not all schools will be able to offer pupils a choice as each unit requires direct teaching and therefore class composition and timetabling may also be relevant factors in the decision. At Higher level there is again a choice of the third unit. A small minority take a statistics unit instead of the main maths unit 3. At Advanced Higher level, there are two courses available. Advanced Higher Mathematics consists of three units covering a range of mathematical skills including algebra, geometry and calculus. Advanced Higher Applied Mathematics allows students the opportunity to study specialised areas of applied mathematics to greater depth. From 2004–05, Advanced Higher Applied Mathematics will consist of two units covering mechanics, numerical analysis and statistics and a third unit of broad content drawn from the Advanced Higher Mathematics course. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.78 | The Scottish Executive considers that the end result of the new NQ courses is that, at each level, schools and students have a wider range of awards available to them and an appropriate choice of courses, while at the same time users of the resulting awards can have confidence about the content of the courses that students will have studied. For mathematics, by far the most common routes for entry to Higher Education are Higher Maths and then, for some students additionally Advanced Higher Maths. Lecturers in HE should not therefore have to contend with a wide range of mathematical background if their classes consist mainly of school leavers. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Core Skills |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.79 | Numeracy is one of five Core Skills within the Scottish Qualifications Framework: the others are Communication, Problem Solving, Working with Others and Information Technology. The core skill of numeracy is defined as follows: “To cope with the demands of everyday life, including work and study, people need to be comfortable with numbers and at ease with graphs, symbols, diagrams and calculators. The skills needed are essentially those of interpreting, processing and communicating quantifiable and spatial information.” Numeracy is regarded as having two components. The first, Using Graphical Information, is described in terms of students progressing from working in familiar, everyday contexts to more abstract contexts where analysis is needed in order to arrive at decisions and communicate conclusions. The second, Using Number, involves the ability to apply a range of numerical and other relevant mathematical and statistical skills in everyday and more abstract contexts. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.80 | All National Qualifications have been audited against the SQA’s Core Skills Framework to determine which core skills are embedded within the assessment arrangements for each unit and course and at what level. Students achieving unit and course awards are automatically certified for the core skills covered by those units and courses. Students also have the option of achieving core skills through dedicated core skills units. These can be achieved in a number of ways – by following a programme of study leading to assessment, by developing a portfolio of evidence or by taking specially designed assessments at an agreed or negotiated time. SQA will be consulting stakeholders in summer 2004 on the future development of all arrangements for assessing and certifying core skills. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pace and Progression |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.81 | As indicated in paragraph 3.70, the Scottish Executive is encouraging schools to think imaginatively and flexibly about how to maximise educational gain for all students. A circular issued in 2001 noted that new National Qualifications offer coherent progression routes between qualifications, some schools may decide to replace some or all Standard Grade provision with these course if appropriate and in accordance with Age and Stage regulations. So far, most schools have not taken full advantage of these new opportunities although some are planning to improve progression routes, for example by moving to Intermediate in S3/4 to improve chances of progression in S5/S6. Initiatives tend to be aimed at mathematically weaker pupils with a view to improving the phasing of work and letting pupils reach a higher level of attainment than previously, albeit at a relatively slow pace. There is less interest in accelerating the most able students as Higher in S5 is still seen as a challenging level for most pupils to reach only a year after Standard Grade in S4. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Examination Arrangements: Role of SQA |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.82 | The SQA is the national body in Scotland responsible for the development,
accreditation, assessment, and certification of qualifications – other
than degrees – and was established under the Education (Scotland) Act
1996, as amended by the Scottish Qualifications Authority Act 2002.
SQA’s functions are to:
SQA is also responsible for developing and distributing 5–14 National Tests to schools as part of the Government’s 5–14 Programme. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Developments |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.83 | Overall, evidence to the Inquiry suggests there is thought to be congruence between stages with the new National Qualification awards in S5/S6 as they have been designed to articulate well with each other and with Standard Grade courses in S3/S4. There is thought to be a lack of congruence between levels A–F within the 5–14 curriculum and Standard Grade/NQs. Level F was designed to articulate to an extent with Intermediate 2, and early in the life of 5–14 some ‘mapping’ was done to identify overlaps between 5–14 and Standard Grade, but this was never completed. Action is underway to address this. The Scottish Executive issued in 2002 National Statements for Improving Attainment in Literacy and Numeracy in Schools. Two national Development Officers have been appointed to support education authorities and schools in making most effective use of the Statements and working with them to improve literacy and numeracy. The remit of the new Numeracy Development Officers includes assisting in the monitoring of good practice in improving progression routes from S1/S2 mathematics courses through S3/S4 and into S5/S6. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.84 | A National Debate on Education was held in Scotland in 2002. The Scottish Executive’s response to the National Debate includes establishing a single set of principles and a framework for the whole curriculum through pre-school, primary and post-primary, looking forward to lifetime learning. Other commitments include consulting on the future of the Age and Stage regulations, addressing the relationship between Standard Grade and new National Qualifications and reducing the amount of time spent on external examinations, including the option of sitting examinations only when leaving school instead of every year from S4. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Terms and Conditions
| Help! |
For further information and to make comments please see the DfES website:
www.dfes.gov.uk/mathsinquiry/