|
|
| 2.1 |
The Inquiry has sought and received input from a wide range of stakeholders.
Not surprisingly, not everyone agrees on every issue relating to post–14
curriculum, assessment, pedagogy and qualifications. But we have identified
one issue on which all stakeholders agree: the absolute necessity of ensuring
adequate provision of appropriately qualified and supported mathematics teachers
in schools, Sixth Form and FE colleges. This is seen by the overwhelming
majority of respondents to the Inquiry to be the essential prerequisite for
delivering long-term future improvements to post–14 mathematics education.
The Inquiry also sees this as the highest priority. |
| 2.2 |
We recognise in relation to our recommendations in this chapter and in
Chapters 5 and 6 that devolved responsibilities for teacher recruitment,
retention, and employment terms and conditions vary across the four territories
of the UK. Responsibilities for teacher supply, training, employment terms
and conditions and Continuing Professional Development (CPD) are fully devolved
to Northern Ireland and Scotland (although Northern Ireland has historically
approached issues of pay and conditions with a view to generally maintaining
parity with arrangements in England and Wales). Wales determines its own
intake targets for Initial Teacher Training and incentives paid to student
teachers, and has devolved responsibility for CPD, but responsibility for
teachers’ terms and conditions remains with the DfES. In relation to
teacher supply, further summary discussion in relation to Wales, Northern
Ireland and Scotland is given at the end of this chapter. |
| 2.3 |
It is also clear that the perception of the problem of mathematics teacher
recruitment and retention varies considerably across the four territories
of the UK. In summary, respondents have raised very serious concerns about
England and Wales, significant concerns about some aspects of the situation
in Northern Ireland, but no serious current concerns about Scotland. Much
of our discussion and analysis will therefore be addressed to the situation
in England and Wales (often, for convenience, using larger volume England
data sources), but often we believe with some relevance to Northern Ireland. |
| 2.4 |
The consensus view of what is an appropriately qualified mathematics
teacher at secondary school and college levels seems well captured by the
categorisations adopted in the 1982 Cockcroft Report, Mathematics
Counts, which are set out in Table 2.1 below. To the categories of those
with good or acceptable qualifications, we would now add those undertaking
the new pre-ITT mathematics enhancement courses (see below paragraphs
2.65–67). |
| |
|
|
Table 2.1: Categories of qualifications of teachers used in the Cockcroft
report
|
| Good |
Trained graduates, or equivalent, with mathematics as the first, main
or only subject of a degree course. Bachelors of Education (BEd) with mathematics
as a main specialist subject. Teachers whose general qualifications were
of either of these types with mathematics as a subsidiary subject provided
their main specialism was in a related subject, such as computer studies,
physics or engineering. |
| Acceptable |
Trained graduates, graduate equivalents, or BEd with mathematics as a
second or subsidiary specialism if their first subject was not related. Untrained
graduates with mathematics as first, main or only subject. Teachers holding
the Certificate in Education, having followed a secondary course in which
mathematics was their first, main or only specialism. Teachers with no initial
mathematical qualifications who had a further qualification resulting from
a course of at least one year in which mathematics was the main subject. |
| Weak |
Teachers holding the Certificate in Education, having followed a secondary
course with mathematics as a second or subsidiary subject, provided their
first or main subject was related. Teachers holding the Certificate in Education
having followed a Junior or Junior /Secondary course with mathematics as
their first or main subject. Teachers in the immediately preceding category
with subsidiary mathematics, provided their main subject was related. Graduates
in any subject provided their course included a related subject. |
| Nil |
Qualified teachers without any recorded mathematics (qualifications)
and not covered by any previous specification. Teachers holding the Certificate
in Education with mathematics subsidiary to an unrelated subject. Teachers
without any initial qualification possessing a further qualification which
did not lead to graduate status and in which mathematics was not the main
subject. |
| Cockcroft, W.H. (1982) Mathematics Counts. London, HMSO. |
|
| 2.5 |
Ensuring adequate numbers of appropriately qualified mathematics teachers
clearly involves both issues of recruitment and retention. This chapter of
the Inquiry report will review the evidence available to us about current
numbers, qualifications and recruitment trends. So far as retention issues
are concerned, respondents to the Inquiry believe that the key issue is that
of professional support, particularly Continuing Professional Development
(CPD). We see this as an important topic in its own right and we will separately
discuss professional support issues in Chapters 5 and 6. |
| |
|
|
|
| 2.6 |
Despite a recent small decline in advertised teacher vacancies and numbers
of temporary teachers employed, a number of respondents to the Inquiry have
reported that many secondary schools and further education colleges in England
and Wales still have considerable difficulty in recruiting and retaining
specialist mathematics teachers. According to the 2000/1 annual report (HMI
0–10–291358–7) of Her Majesty’s Chief Inspector of Schools:
“In Mathematics: there are insufficient teachers to match the demands
of the mathematics curriculum in one school in eight, a situation that has
deteriorated from the previous year.”
The Chief Inspector’s report for 2001/2 (HMI 0-10-292032-X) states that:
“Across secondary schools there remain significant difficulties in the
recruitment of specialist teachers, particularly, but not exclusively, in
mathematics … These recruitment difficulties are having an adverse impact
on pupils’ standards of achievement. For example: the quality of mathematics
teaching at Key Stages 3 and 4 suffers in many schools because the limited
amount of specialist teachers’ expertise is deployed largely on
post–16 courses. As a result, non-specialist teachers undertake a
significant minority of the teaching at Key Stage 3, where they find it difficult
to respond effectively to the demands of the Key Stage 3 Strategy.”
|
| 2.7 |
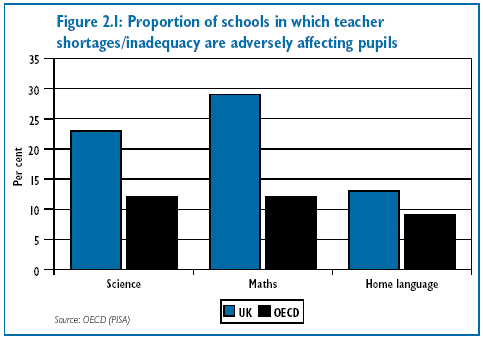
The Inquiry notes with concern the Chief Inspector’s view in 2001/02
that shortages of specialist teachers in mathematics are having an adverse
effect on pupils’ performance. This is a view echoed by many respondents
to the Inquiry and further supported by data presented in the SET for
Success report. Figure 2.1 below (which reproduces Figure 2.14 of the
SET for Success report), shows the proportion of head teachers in
an OECD study who believe that teacher shortage or inadequacy is hindering
the learning of pupils in different subjects. The Inquiry notes that, according
to this survey, the position of mathematics is strikingly worse in the UK
than in other OECD countries. |
|
 |
| 2.8 |
This concern about the effect of the shortage of specialist teachers
on students’ learning of mathematics has been echoed by almost all
respondents to the Inquiry. In England, Ofsted, the Teacher Training Agency
(TTA), headteachers and mathematics teaching professionals have all communicated
their concern. The General Teaching Council for Wales (GTCW) has expressed
concern that in Wales secondary school posts in mathematics attract significantly
fewer applicants than for many other subjects. Surveys in Northern Ireland
have shown there to be significant concerns about the situation in non-grammar
schools and even some concern regarding recruitment to grammar schools The
Inquiry shares these concerns. In our view, the very highest priority in
tackling the mathematics problem is to increase the supply of mathematically
qualified, effectively trained specialist mathematics teachers. There are
considerable difficulties in addressing this supply problem and we can fully
understand that those confronting the problem must sometimes despair and
be led to seek other solutions, which involve the deployment of non-specialist
staff. We note, however, the contrast with the view taken in Scotland, where,
since 2000/01, teachers of mathematics have been required to have studied
the subject for three years at university. |
| 2.9 |
The Inquiry urges the DfES and the LSC to continue to acknowledge the
importance of specialist teachers in mathematics and to accept that increasing
the supply of specialist teachers of mathematics is an essential component
of any strategy for tackling the mathematics problem in English schools (DfES)
and colleges (LSC). We similarly urge the relevant authorities in Wales and
Northern Ireland to give the issue the very highest priority and to consider,
where appropriate, whether they might wish to implement their own versions
of recommendations made for the English context. The rest of this chapter
of the report focuses on what we perceive to be the scale of the problem
of under-supply in England and ways in which we believe, over time, that
supply can be increased. |
| |
|
|
|
| 2.10 |
Official estimates of the numbers, age, profile and qualifications of
teachers of mathematics in secondary schools in England are based on the
Secondary Schools Curriculum and Staffing Survey (SSCSS). Until 1996, the
Secondary SSCSS was conducted at four-yearly intervals. However, the Inquiry
has noted with concern that the most recent SSCSS took place after a six-year
interval, with a closing survey date of 21 November 2002. Some preliminary
findings on qualifications and age profile have been released from the 2002
SSCSS and will inform our attempts to analyse trends. However, these findings
are in the form of percentage breakdowns and we regret that key data on absolute
numbers are not available for inclusion in this report. |
| 2.11 |
From the 1996 Survey, it was estimated that there were 27,100 full-time
and 3,700 part-time teachers in secondary schools with a post A-level
qualification in mathematics. Not all of these were engaged in full-time
mathematics teaching, but of the 25,200 full-time teachers actually teaching
mathematics in years 7–13, 20 per cent had no post A-level qualification
in mathematics. The number of teachers with a post A-level qualification
teaching mathematics was 20,160 in 1996. |
| 2.12 |
One interesting inference from these figures is that in 1996 there appear
to have been nearly 7,000 teachers in secondary schools with a post A-level
qualification in mathematics who were not teaching mathematics. This is of
the order of 25 per cent of the qualified cohort within schools. Some of
these teachers may, of course, have moved to teach other subjects –
for example, computer studies. However, it seems very unlikely that this
accounts for more than a fraction of the large numbers of qualified teachers
no longer teaching mathematics. This seems to the Inquiry to raise serious
issues about current school level resource management and the incentives
for qualified subject teachers to remain teaching their subject rather than
moving into other posts. |
|
Recommendation 2.1
The Inquiry recommends that the DfES undertake a review of school level resource
management of qualified mathematics teachers in England. This review should
include an assessment of whether current career paths and rewards provide
appropriate incentives for qualified mathematics teachers to continue teaching
mathematics. The LSC might wish to consider a similar exercise regarding
the deployment of qualified mathematics teachers in colleges. |
| 2.13 |
It has been suggested to the Inquiry that, in considering issues of qualified
teacher supply in secondary schools, we should base our analysis solely on
those actually teaching mathematics rather than on the total numbers with
a post A-level qualification, since the latter include many teachers who
are not currently teaching mathematics. This seems to us to ignore two important
points. First, it disregards the potential for increasing the pool of qualified
mathematics teachers actually teaching mathematics within schools by making
suitable changes to school level resource management practices and incentives
for teachers to remain teaching their subject. Secondly, it does not take
on board that if future trends continue to reflect the fact that something
like a quarter of post A-level qualified mathematics teachers eventually
end up not teaching mathematics this needs to be factored into projections
and strategies for mathematics teacher recruitment. |
| 2.14 |
The 1996, 1992 and 1988 surveys revealed a worrying trend in the number
of teachers qualified in mathematics as shown in Table 2.2. Some of the decline
from 1992 will be due to the transfer of Sixth Form Colleges from the Schools
to the FE Sector during the period after the 1992 survey. However, even allowing
for this, the figures suggest a significant decline over the period in the
number of qualified mathematics teachers in secondary schools. It is therefore
a cause of considerable concern to the Inquiry that up to date numbers are
not available to us from the 2002 SSCSS. |
|
Table 2.2: Survey numbers of qualified mathematics teachers in maintained
secondary schools in England and Wales
|
| Survey |
Teachers qualified in Mathematics (full and part-time) |
| 1996 Survey |
30,800 |
| 1992 Survey |
43,900 |
| 1988 Survey |
46,500 |
|
| 2.15 |
The Inquiry believes that a clear understanding of trends in the provision
of qualified mathematics teachers is a key prerequisite to informed policy
making regarding mathematics teacher recruitment and retention. The Inquiry
therefore has further serious concerns about the low response rates in these
recent surveys. The 1996 survey was based on a sample of 553 secondary schools
and achieved a response rate of 60 per cent. The 2002 survey was based on
a sample of 883 schools and achieved a response rate of 24 per cent. The
DfES response to the Inquiry’s concern regarding these low response
rates has been to argue that they are a direct consequence of the excessive
burdens that such surveys place on schools. The Inquiry notes this argument,
but regards it as defeatist and unhelpful. We are absolutely convinced that
policy making in this area requires good quality data and we urge the DfES
and the LSC to accept and take forward Recommendation 2.2 below. |
| 2.16 |
In the absence of key numbers from the 2002 survey, the Inquiry has examined
alternative approaches to quantifying the current situation regarding numbers
of qualified mathematics teachers. Estimates supplied to the Inquiry by the
DfES suggest an outflow from maintained secondary schools in England and
Wales in the period 1996 to 2003 of just over 8,900 teachers with a post
A-level mathematics qualification actually teaching mathematics. Over the
same period, the total inflow with a post A-level mathematics qualification
has been just over 7,300. As we have seen from the 1996 figures, we can infer
that something like 25 per cent of the teacher cohort qualified to teach
mathematics ends up not actually teaching mathematics. Applying this to the
inflow figure of 7,300 given above, we would estimate that this corresponds
in the steady state to an addition of around 5,500 to the cohort of qualified
mathematics teachers who will actually be teaching mathematics, The decline
over the period of qualified mathematic teachers actually teaching mathematics
is likely therefore to have been of the order of around 3,400. |
| 2.17 |
It is not clear how schools have been able to cope with the shortfalls
without an increased use of unqualified teachers. The 2002 Curriculum Survey,
published in April 2003, shows mathematics still being taught to 100 per
cent of pupils in Years 7–11, with no apparent change in the time allocated
to the subject in any of the year groups. We note that the survey does not
provide information on the number of pupils in teaching groups. Overall in
secondary schools, class sizes seem to have remained relatively constant,
but anecdotal evidence to the Inquiry suggests that class sizes in many sixth
forms and FE Colleges have been increasing significantly. There are other
changes that have impacted further upon the numbers of qualified mathematics
teachers in schools and colleges. In particular, respondents to the Inquiry
have estimated that the mathematics strand of the KS3 Strategy has resulted
in at least some 300 experienced secondary mathematics teachers being taken
out of schools since 2001 to support this initiative. |
| 2.18 |
It is clear that the non-occurrence of the SSCSS survey in 2000 and the
need to place continued reliance on the 1996 data has caused considerable
concern to the many stakeholders already worried about the supply of qualified
mathematics teachers. This has led in the interim to several attempts at
unofficial surveys of the position. In 2001, a joint group from The Open
University, King’s College London and the National Association of
Mathematics Advisors (NAMA) carried out a survey1 of all NAMA members in
a mix of metropolitan, unitary and shire counties across England. A total
of 228 schools responded from 22 LEAs, involving a mixture of 1,571 full-time
and part-time teachers of mathematics. |
| 2.19 |
In addition, Willis (2002)2 surveyed 54 schools involving
364 mathematics teachers on behalf of the Secondary Headteachers Association
(SHA) and Roper (2002)3, using the same definitions as the NAMA
survey, surveyed 158 schools involving 536 mathematics teachers. The Inquiry
has significant reservations about the unofficial and small-scale nature
of these surveys. We also have a concern about response rates, a concern
that also applies to the SSCSS 2002 survey, as noted above. However, to the
extent that response bias in this context is felt by many respondents to
be likely to lead to an understatement of the problem, the surveys may be
indicative and we feel, on balance, that the outcomes are worth reporting.
To facilitate comparisons with earlier studies, the data from the NAMA survey
were analysed by the authors using the same categories as in the Cockcroft
report (see Table 2.1). |
| 2.20 |
The OU/KCL/NAMA report makes clear that it is not the intention of the
authors that the terms ‘good’, ‘acceptable’,
‘weak’ be seen as necessarily applicable to every individual teacher
whose qualifications fall in the relevant category. The assumption is rather
that the overall picture based on this categorisation provides a meaningful
measure of the extent of the shortage of specialist mathematics teachers.
The Inquiry agrees that the measures used in these surveys do provide a
reasonable aggregate basis for quantifying the shortage of appropriately
qualified mathematics teachers. |
| 2.21 |
Results of the OU/KCL/NAMA survey (see Table 2.3) show that, in the schools
responding, nearly 24 per cent of those teaching mathematics had
‘weak’ or ‘nil’ qualifications in mathematics. The survey
also revealed a number of school mathematics departments with large numbers
of part-time teachers teaching mathematics. Overall, the schools reported
that 8 per cent of mathematics teachers were about to retire. Of the 504
teachers who taught AS or A-level, 34 (nearly 7 per cent) had A-level as
their highest mathematics qualification and 3 had no higher qualification
than GCSE. |
|
Table 2.3: Qualifications of mathematic teachers
|
| Good |
916 |
58.3 per cent |
| Acceptable |
230 |
14.6 per cent |
| Weak |
100 |
6.4 per cent |
| Nil |
275 |
17.5 per cent |
| Not reported |
51 |
3.3 per cent |
|
| 2.22 |
There are a significant number of part-time teachers of mathematics in
secondary schools. In order, therefore, to get an estimate of how much teaching
is carried out by teachers with ‘weak’ or ‘nil’ initial
mathematics qualifications it is necessary to consider the percentage tuition
time rather than just teacher numbers in each category. This results in the
estimates given in Table 2.4. These estimates suggest that, among the schools
responding, 14.6 per cent (one in seven) of secondary mathematics lessons
in England are taught by teachers with ‘weak’ or ‘nil’
mathematics qualifications. |
|
Table 2.4: Qualifications of mathematic teachers by hours of teaching
|
| Good |
17570 |
69.2 per cent |
| Acceptable |
4116 |
16.2 per cent |
| Weak |
1221 |
4.8 per cent |
| Nil |
2480 |
9.8 per cent |
|
| 2.23 |
Willis (2002) also estimated that 14 per cent of mathematics lessons
(one in seven) were taught by a teacher not qualified to teach mathematics,
although we note that his definition of “qualified” was not as
stringent as the OU/KCL/NAMA definition. Roper (2002) also estimated that
14 per cent of mathematics teachers were not properly qualified to teach
mathematics. This latter survey, unlike the other two, also included independent
schools. Assuming a pupil to teacher ratio of 17.0 in maintained secondary
schools in England (the January 2003 figure reported in SFR 23/2003) and
assuming that around 13 per cent of the curriculum is devoted to mathematics,
the OU/KCL/NAMA report calculates that some 25,900 full-time equivalent
mathematics teachers are needed for the secondary school sector. The OU/KCL/NAMA
report concludes, therefore, that just under 3,800 mathematics teachers need
to be trained or brought into the system to cover the posts currently filled
by teachers with ‘weak’ or ‘nil’ mathematics qualifications.
Notwithstanding concerns about the unofficial nature of the surveys, sample
sizes and response rates, the Inquiry believes that the analyses summarised
above provide a prima facie case for estimating there to be a current shortfall
of 3,400–3,800 qualified mathematics teachers teaching mathematics in
secondary schools in England. |
| 2.24 |
The OU/KCL/NAMA survey also collected data, Table 2.5 below, on the
experience of schools trying to recruit teachers of mathematics. Respondents
clearly felt that the number of applicants for mathematics teaching posts
with ‘good’ or ‘acceptable’ mathematics qualifications
continues to decline. Some schools reported advertising for five or six teachers
during a single year. Over a quarter advertised for three or more mathematics
teachers during the year. Overall, only 37.1 per cent of the appointments
made by those schools responding to the survey were considered to be of teachers
with ‘good’ mathematics qualifications. |
|
Table 2.5: Results of advertisements in the year 2001–2002
|
| Good appointment |
136 |
37.1 % |
| Satisfactory appointment |
70 |
19.1 % |
| Appointment needing support |
40 |
10.9 % |
| Unsatisfactory appointment – no choice |
39 |
10.6 % |
| No appointment made – staff moved |
77 |
21.0 % |
| Vacancy |
5 |
1.4 % |
|
| 2.25 |
The SSCSS also collects data on teacher qualifications. However, the
Inquiry is concerned that current categorisations used in the SSCSS survey
do not permit clear inferences to be drawn. The SSCSS estimated the percentages
of teachers of mathematics who hold no qualifications in mathematics higher
than A-Level to be around 20 per cent in 1996 rising to 26 per cent in 2002.
However, the categorisation used in the survey only indicates the lack of
a mathematics degree. It does not distinguish between other degrees with
a high mathematical content (eg physics) and those with low mathematical
content. This ambiguity is reflected in the Secretary of State’s 25
September, 2003, press statement regarding the 2002 SSCSS:
“A proportion of mathematics teachers are listed in the survey as having
‘no qualification in mathematics’; but this does not mean they
are unqualified. Most of these teachers are likely to be qualified and graduates
in subjects such as physics .... They may only teach one or two periods of
mathematics a week.”
|
| 2.26 |
The Inquiry would be considerably reassured to know that this was the
case, although we might have concerns about these teachers’ knowledge
of and exposure to mathematics pedagogy if their specialist training had
been in a different subject. However, we find it frustrating and unsatisfactory
that such issues are currently matters of speculation rather than being clearly
evidencebased. To achieve the latter, we need clearer categorisation in the
survey, perhaps based on the Cockcroft categorisation, in order to distinguish
qualifications with appropriate mathematics content from those lacking such
content (see Recommendation 2.2 below). |
| |
|
|
|
| 2.27 |
We also note that the SSCSS relates solely to teachers of mathematics
in maintained secondary schools. However, there are a significant number
of teachers of mathematics in independent schools and Sixth Form and FE Colleges.
In relation to colleges, the Inquiry notes that the LSC currently has no
equivalent of the SSCSS data on numbers and qualifications of teachers of
mathematics. Data in colleges are currently collected in the categories used
for Ofsted inspections, for which mathematics numbers are subsumed within
the science category and are not separately identifiable. We view this absence
of data with some concern in view of a number of developments that are likely
to increase demands on mathematics teaching resources in colleges. For example,
DfES evidence to the Inquiry acknowledges that progress on the adult numeracy
strategy could be undermined by the limited pool of competent and confident
teachers of mathematics and numeracy currently available in the adult sector.
This task of addressing the lack of numeracy skills among a large section
of the adult population will require additional staff with mathematics
qualifications to provide support to trainers, even if they are not used
to deliver the programme. There is also the risk that any shortage might
be met by further leakage from the secondary and FE sectors. It has also
been suggested to the Inquiry that teaching interested adults may seem more
appealing to some current schoolteachers than working with sceptical adolescents.
This might result in further losses of mathematics teachers from the secondary
school sector. |
| 2.28 |
However, as there appear to be no national targets for lecturer supply
and training in colleges, it is difficult to quantify the effects of these
additional pressures on the demand for mathematics educators. The Inquiry
regards it as extremely unhelpful that in the key area of mathematics teacher
supply there is currently no coherent overall understanding of numbers and
qualifications (see Recommendation 2.2 below). |
| |
|
|
|
| 2.29 |
Respondents to the Inquiry have also expressed anxieties about the future
capacity and availability of suitably qualified mathematics educators in
higher education to deliver quality ITT and provide ongoing CPD. Trainers
themselves clearly need to be appropriately academically qualified and to
continue to update their own knowledge and skills in order to properly train
future teachers. The Inquiry has therefore noted with considerable concern
that there does not seem to be an evidence base relating to the numbers and
profile of those delivering mathematics teacher training. |
| 2.30 |
The results of an informal survey carried out in May 2002, by the University
Council for the Education of Teachers suggest that there are serious problems
ahead. Higher Education Institutions with ITT provision were asked to return
the numbers and ages of staff working in mathematics education. Of the trainers
covered by these responses, 63 per cent trained primary teachers, 40 per
cent trained secondary teachers and 17 per cent trained post–16 teachers
(with some overlap). The age profile of those trainers covered by the providers
responding to the survey is shown in Table 2.6. Given the relatively low
response rate (58 per cent) and some problems with inconsistencies in responses,
the Inquiry is not sure how much weight to attach to these figures. However,
if they are at all representative, the Inquiry has concerns for the future
of a system in which 50 per cent of the current trainers are over 50 years
of age. |
|
Table 2.6: Age profile of teacher trainers
|
| Age |
26–30 |
31–35 |
36–40 |
41–45 |
46–50 |
51–55 |
56–60 |
61–65 |
| No. of staff |
4 |
10 |
9 |
14 |
25 |
40 |
24 |
2 |
|
| |
|
The need for up-to-date comprehensive data
|
| 2.31 |
At all levels, the Inquiry has serious concerns about the current evidence
base regarding the numbers and profile of those teaching post–14 mathematics
in schools, Sixth Form Colleges and FE Colleges and providing mathematics
ITT. This evidence base is crucial for understanding current and future supply
needs for teachers of mathematics at all levels and for monitoring progress
towards meeting these needs. This prompts the following recommendation, expanding
on Recommendation 2.1, which we would wish to be taken on board by relevant
bodies, including the National Statistics Strategic Review of School Workforce
Statistics, which we understand is due to report in 2004. |
|
Recommendation 2.2
The Inquiry recommends that the DfES and the LSC work together and
with the TTA to review the frequency and scope of data collection relating
to mathematics teacher and teacher trainer numbers and qualifications. They
should seek to agree a data collection strategy that will provide the evidence
base for a coherent policy approach to the supply of appropriately qualified
teachers for the teaching of mathematics across all secondary schools, sixth
form and further education colleges, and of appropriately qualified
ITTmathematics trainers. In particular, the Inquiry recommends that:
-
(i) a revised form of SSCSS, requiring a mandatory response, should be designed
and undertaken as soon as possible to cover not only secondary schools, including
those in the independent sector, but also sixth form and furthereducation
colleges and providers of mathematics ITT;
-
(ii) categories of response be redefined, along similar lines to the Cockcroft
categorisation, to provide a clearer indication of teacher qualifications;
-
(iii) the breakdown of qualifications should be available separately for
the those teaching key skills, KS3, KS4 and post–16;
-
(iv) in view of the current critical position in regard to provision of teachers
of mathematics and the need for close monitoring of policy initiatives to
improve recruitment and retention, at least the first three new surveys should
be undertaken every two years.
|
| |
|
|
|
| 2.32 |
Vacancy rates provide another source of data for assessing the extent
to which there is a shortage of specialist mathematics teachers. Technically,
a vacancy is defined as a post that has been advertised for a full-time permanent
appointment (or appointments of at least one-term’s duration) but has
not been filled. This includes posts that are being filled on a temporary
basis of less than one term. Part-time posts and fixed-term posts that are
unfilled are not counted as vacancies, nor are posts that are filled on a
temporary basis for one term or more, for example by agency staff. |
| 2.33 |
Despite recent improvements, analysis of data on vacancies as a percentage
of teachers in post confirms that the shortage in teachers of mathematics
is more acute than for many other subjects. Concerns about the supply of
mathematics teachers in the period 1997–2003 are reflected in evidence
provided to the Inquiry by the DfES. Figure 2.2 below illustrates trends
in vacancy rates for mathematics compared with a selection of other subjects,
and with the aggregate over all subjects in maintained secondary schools
in England since 1997. The graph for mathematics reveals an overall rise
in the vacancy rate from a level of just under 0.5 per cent of the 1997
mathematics teacher stock, to a peak rate of 2.1 per cent in 2001. In 2002,
there was a small decline to 1.9 per cent and in 2003, a further decline
to 1.7 per cent. This recent downward trend is encouraging. However, the
Inquiry notes that the 2003 rate is still the third highest vacancy rate
for mathematics teachers in the past decade and also the second highest for
all the other subjects in 2003. |
|
 |
| 2.34 |
Reported numbers of vacancies provided by the DfES to the School Teachers
Review Body (STRB) are shown in Figure 2.3. The Inquiry welcomes the recent
downward trend but again notes that the current numbers are still well above
the average of the 1990s, even as a proportion when increased teacher numbers
are taken into account. |
|
 |
| 2.35 |
Figure 2.4 shows the number of advertisements for mathematics teachers
in England that have appeared in the Times Educational Supplement (TES) in
the past five years. This prima facie evidence further supports the view
that unfilled teacher vacancies have been reducing in number; certainly,
there are fewer advertisements than two years ago. The Inquiry again welcomes
this trend but remains concerned that the data do not show the extent to
which there is still a latent demand for more qualified mathematics teachers
in schools where a significant proportion of lessons are taken by unqualified
teachers. |
|
 |
| 2.36 |
So far as turnover of staff is concerned, surveys conducted by the National
Employers’ Organisation for School Teachers, with support from the DfES
and the teacher unions, collect information on resignations by teaching subject.
This, combined with information about the number of staff by main teaching
subject from the SSCSS, provides the basis for calculating turnover rates.
In 2001, the turnover rate for secondary mathematics teachers in England
was 15.3 per cent. The Inquiry notes with concern that this was twice that
of 1991 (7.6 per cent) and higher than the 13.5 per cent average turnover
rate for secondary teachers. Provisional data for 2002, supplied to the Inquiry
by the DfES, suggest a small improvement in turnover rate for secondary
mathematics teachers of 13.6 per cent against an average for all subjects
of 12.5 per cent. |
| |
|
|
|
| 2.37 |
International comparisons reported in the Roberts report (SET for
Success, paragraph 2.44) suggest that although other countries also
experience more shortages of teachers in science and mathematics than in
other subjects, the shortages in the UK are considerably worse than elsewhere.
Furthermore, teacher shortages in mathematics (as well as physics, chemistry
and design Technology) could well worsen over time, since, as shown in Figure
2.5 (Figure 2.13 of SET for Success), fewer teachers whose main
qualification is in these subjects are under 30 and more are over 50 compared
with their counterparts in other subjects. |
|
 |
| 2.38 |
A further serious problem for the future arises from trends in the age
profile of the mathematics teaching profession. Data from the SSCSS revealed
that the position was already worrying in 1996. However, provisional data
released from the 2002 SSCSS shows a further marked deterioration in the
age profile of mathematics teachers. Of the full-time teachers surveyed in
1996, 63 per cent were over 40 compared with 60 per cent of all secondary
teachers; 20 per cent were over 50, compared with 17 per cent of all secondary
teachers; 15 per cent were under 30 compared to 16 per cent overall. According
to the 2002 SSCSS, 62 per cent were over 40, compared with 56 per cent of
all secondary teachers; 31 per cent were over 50, compared with 27 per cent
of all secondary teachers; 16 per cent were under 30, compared with 20 per
cent overall. Figure 2.6 provides a comparison of the 1996 and 2002 age profiles. |
|
 |
| 2.39 |
The shift in age profile of the population of full-time mathematics teachers
in secondary schools revealed by the 2002 SSCSS is a cause of major concern
to the Inquiry. In particular, we would like to be reassured that this
demographic shift is being fully taken into account in modelling future demand
and calculating future mathematics teacher training requirements for the
whole system in England. As indicated earlier, we cannot see how coherent
forecasts can be made at present given the apparent lack of age profile data
for those teachers of mathematics working in Sixth Form and FE Colleges.
We are also concerned that even existing surveys only cover the maintained
secondary school sector and do not factor in the numbers of mathematics teachers
required in the independent sector. |
|
Recommendation 2.3
The Inquiry recommends that at the earliest possible opportunity forecasts
of future teacher training number requirements for mathematics teachers be
re-examined in the light of:
-
the estimate we have suggested of a current shortfall of at least 3,400 qualified
mathematics teachers in secondary schools;
-
the age profile findings from the 2002 SSCSS;
-
and taking into account the current position and future needs of independent
schools, Sixth form and FE Colleges, in addition to secondary schools.
|
| |
|
|
|
| 2.40 |
Perhaps the cause of greatest concern to many respondents to the Inquiry,
and not only in the context of teacher recruitment, has been the dramatic
decline in A-level mathematics entries since the Curriculum 2000 changes
were introduced. This is shown in Table 2.7. |
|
Table 2.7: Total A-level entries (all UK, all ages)
|
| Year |
Numbers of candidates |
| 2003 |
55,917 |
| 2002 |
53,940 |
| 2001 |
65,891 |
| 2000 |
65,836 |
| 1999 |
68,502 |
| 1998 |
68,846 |
| 1997 |
68,853 |
| 1996 |
67,022 |
| Source: JCGQ. |
|
| 2.41 |
The decline in the number of candidates in the period 2000–2003
is of the order of 15 per cent. Respondents have seen this as having serious
potential consequences for recruitment into mathematics and other degree
courses with high mathematics content, with subsequent problems in two and
three years time for recruitment into mathematics teacher training. However,
data on numbers entering into undergraduate mathematics courses, shown in
Table 2.8 below, present some mixed messages. |
|
Table 2.8: Entry to undergraduate mathematics (all UK)
|
| Year |
Applicants |
Acceptances, including clearing applications |
| 2003 |
3825 |
4329 |
| 2002 |
3325 |
3840 |
| 2001 |
3863 |
4006 |
| 2000 |
3925 |
4052 |
| 1999 |
3989 |
4158 |
| 1998 |
3887 |
4147 |
| 1997 |
3816 |
4255 |
| 1996 |
3839 |
4159 |
|
| 2.42 |
There was, indeed, a sharp drop in applications in 2002, of around 14
per cent, which translated into a subsequent 4 per cent drop in numbers entering
mathematics degrees. However, in 2003 the number of applications has increased
back to around the 2001 level and, perhaps surprisingly, the number of entries
to degree courses actually increased significantly to one of the highest
levels for a decade, although we note that this still only represents a return
to the level of the mid–1990s. The figures for 2003 have only become
available as this Inquiry was completing its work. We have therefore had
no opportunity to investigate the rather volatile movements in numbers over
the past couple of years. Some respondents to the Inquiry have suggested
that this sudden increase may be explained by internal funding issues within
HEIs linked to student recruitment problems in some mathematics departments.
This may have led to changed (ie a lowering of) entry requirements in some
institutions. The Inquiry has not been able to follow up on this suggestion,
but we suggest that it would be valuable for someone to investigate further
these patterns of applications and acceptances. We suggest that the Committee
of Heads of Departments of Mathematical Sciences in Higher Education (HoDMS)
might undertake such an investigation, perhaps in conjunction with the Council
for the Mathematical Sciences. |
| |
|
|
|
| 2.43 |
Evidence to the Inquiry from the TTA shows that, in recent years, newly
qualified teachers have made up 45 per cent of the total inflow of all teachers
into the secondary maintained sector. Overall, in secondary schools in 2001
there was a staffing inflow of 9 per cent and an outflow of 8 per cent. This
fine balance between inflow and outflow makes it essential to ensure that
a good supply of newly qualified teachers is maintained and therefore that
able and committed trainees are recruited to fill all allocated training
places. We are aware that the DfES is currently consulting on proposals for
reform of ITT in FE, following a critical review by Ofsted. We urge that
careful consideration is given to ensuring that, where appropriate, the
recommendations we make in this chapter are also implemented in that context. |
| 2.44 |
Teachers working in maintained schools in England normally hold Qualified
Teacher Status (QTS), which is usually obtained through completing ITT. There
are three main routes for achieving QTS:
-
as part of an undergraduate degree BEd, BA or BSc (mostly used for primary
school teachers);
-
through a postgraduate training course, often combined with study for a
Postgraduate Certificate in Education (PGCE);
-
for trainees via employment in schools on the Graduate Teacher Programme
(GTP) or the Registered Teacher Programme (RTP) (for those without a first
degree but with two years’ study in higher education).
|
| 2.45 |
Postgraduate trainee teachers in England and Wales on an eligible ITT
course receive a £6000 training bursary as a recruitment incentive.
The TTA also administers a Secondary Subject Shortage Scheme. An additional
£4,000 is available for eligible postgraduates who go on to teach in
shortage subjects in England4, and some further training awards
are available to secondary school teacher trainees in shortage subjects based
on financial need5. Some of these incentives are also available
in Wales. The following table (Table 2.9) shows the kinds of routes and financial
provision available to potential mathematics teachers. |
|
Table 2.9: A summary of current training routes
|
| Route |
Time |
Training bursary |
Undergraduate routes
BA with QTS or BSc with QTS |
1 term – 1 year (QTS) |
|
Postgraduate routes
Postgraduate Certificate
in Education (PGCE) |
1 year full-time.
Part-time varies |
£6,000 |
| PGCE (flexible) |
10 weeks – 2 years |
£6,000 max |
| PGCE (2-year) |
2 years |
£6,000 in final year only |
| Fast track |
1 year enhanced PGCE with extended development in school |
£6,000 + additional £5,000 |
Employment based routes
Graduate Teacher Programme (GTP) |
1 term – 1 year |
£13,266 salary |
| Registered Teacher Programme (RTP) |
1 – 2 years |
£13,266 salary |
| Overseas Trained Teachers Programme (OTTP) |
Up to 1 year |
£13,266 salary |
|
| |
|
Undergraduate routes
|
| 2.46 |
The Inquiry notes that undergraduate teacher training courses are now
of declining importance as a route for training secondary mathematics teachers
(Figure 2.7 below). |
|
 |
| |
|
Mainstream PGCE recruitment
|
| 2.47 |
The mainstream ITT PGCE courses continue to be the most important route,
with improved recruitment in recent years as shown in Figure 2.8. In 2003/04
95 per cent of entrants to secondary mathematics ITT (excluding the
employment-based routes) were postgraduates. The Inquiry very much welcomes
the increased mathematics teacher training enrolment over the past five years.
The postgraduate recruitment in 2002/3 was the highest since 1994/5. However,
we are also mindful that the recruitment level is only just recovering to
that of 1996/97 (1,653), which itself represented a significant decrease
compared to the level of the previous year, 1995/96 (1,795). |
|
 |
| |
|
Flexible PGCE recruitment
|
| 2.48 |
In addition to the standard, usually one-year and full-time, PGCE course,
a flexible or modular PGCE has been recently introduced, designed to meet
the needs of trainees with commitments that preclude other than a part-time
route. The course can be taken over a period of up to two years but may be
completed in a shorter time (a minimum of six weeks) by trainees with suitable
relevant prior experience. The distinctive feature of courses designated
as flexible is that they have variable start and finish points. Over the
last three years, the number of flexible mathematics ITT places in England
has increased by 23 per cent (from 212 places in 2001/02 to 260 in 2003/04).
From September 2003, there will be around 40 HE providers offering such courses. |
| |
|
Employment-based routes
|
| 2.49 |
Employment-based routes are beginning to make a significant contribution
to the number of people training to teach mathematics (see Figure 2.9). The
Graduate Teacher Programme (GTP) is a programme that allows graduates to
earn a salary while they train to be a teacher. Since September 2003 GTP
has been open to applicants of any age. The GTP enables schools to employ,
as supernumeraries, people who do not yet have QTS and train them through
an individual training programme leading to QTS. Schools are funded to pay
GTP trainees as unqualified teachers, a minimum of £13,266 a year, whilst
they are training. The programme is designed for individuals who want to
change to a teaching career but need to continue earning while they train.
The Registered Teacher Programme (RTP) offers individuals the opportunity
to work as an unqualified teacher in a maintained school in England whilst
completing the final year of a degree and undertaking teacher training.
Individuals who have qualified as a teacher outside the European Economic
Area may gain QTS through the Overseas Trained Teacher Programme (OTTP) while
working as a teacher. While on the OTTP trainees follow an individualised
training programme leading to QTS while working in a school as an unqualified
teacher. |
|
 |
|
The GTP is the most significant of the employment-based routes. In response
to the increases in recruitment through this route, Ministers have agreed
to double the size of the GTP by 2005/06. In addition to the GTP numbers,
the RTP has contributed 19 new teachers of mathematics and the OTTP has
contributed 175. The Inquiry very much welcomes this response and would wish
to see further increases if demand for this route continues to grow and quality
is assured. |
| |
|
Overall recruitment
|
| 2.50 |
The total annual number of new mathematics trainees from 1998/99 to 2002/3
is shown in Figure 2.10. |
|
 |
| 2.51 |
Factors that the TTA believes have contributed to the increased interest
in and subsequent rise in postgraduate recruitment numbers in recent years
include:
-
the introduction of training bursaries and ‘golden hellos’;
-
the penalties imposed for under-recruitment;
-
a more vigorous communications and marketing campaign;
-
impressing on ITT providers the importance of recruiting to all the allocated
places;
-
a wider range of teacher training opportunities.
|
| 2.52 |
The Inquiry welcomes these recent increases in numbers entering teaching
training in mathematics as well as the upward trend in the number of training
places available. However, we note that there remains a considerable shortfall
in recruitment compared with the training places available. Figure 2.11 below
shows the number of mathematics training places available each year from
1990/91 and Figure 2.12 shows the percentage of places filled, the latter
clearly reflecting the effects of the economic cycle. The number of ITT places
for mathematics in 2003/04 is 2,350. |
|
 |
|
 |
| |
|
Comparisons with recruitment in other subjects
|
| 2.53 |
Tables 2.10 and 2.11 indicate the considerable difficulties experienced
in recruiting to mathematics teacher training compared with some other subjects.
These recruitment figures exclude fast track trainees. |
|
Table 2.10: Places and actual recruitment for Initial Teacher Training in
England, 2002/03
|
| Subject |
Actual recruitment |
Places |
Proportion of places filled |
| Mathematics |
1,673 |
1,940 |
86 per cent |
| Science |
2,701 |
2,850 |
95 per cent |
| Modern Languages |
1,732 |
2,050 |
84 per cent |
| English & drama |
2,479 |
2,350 |
105 per cent |
| History |
985 |
950 |
104 per cent |
|
|
Table 2.10: Places and actual recruitment for Initial Teacher Training in
England, 2003/04
|
| Subject |
Actual recruitment |
Places |
Proportion of places filled |
| Mathematics |
1,951 |
2,315 |
84 per cent |
| Science |
2,854 |
3,225 |
88 per cent |
| Modern Languages |
1,815 |
2,050 |
89 per cent |
| English & drama |
2,440 |
2,350 |
104 per cent |
| History |
994 |
950 |
105 per cent |
| Sources: Recruitment – TTA ITT trainee
number census, 2003 |
|
| 2.54 |
Figure 2.13 below shows trends in the percentage of available teacher
training places filled in secondary mathematics along with those for English,
science and the aggregate over all secondary subjects. |
|
 |
| 2.55 |
The Inquiry notes that, according to figures supplied by the DfES, at
present only around 66 per cent of applicants in mathematics make it onto
PGCE courses. This compares, for example, with 98 per cent on design and
technology, 82 per cent on music and 79 per cent on RE courses. Mathematics
has a conversion rate from applicant to trainee that is closer to subjects
such as English (53 per cent), where there is a plentiful supply of applicants.
This raises the question of whether ways could be found to enable more of
the 1,000 applicants who are currently turned away, or withdraw their
applications, to become mathematics trainees and eventually teachers. We
suggest that the TTA, together with ITT providers might investigate this
relatively low conversion rate from mathematics PGCE applicant to trainee. |
| |
|
Comparisons with qualifications of trainee teachers in other subjects
|
| 2.56 |
So far as the academic qualifications of entrants to mathematics teacher
training is concerned, over the period 1996/97 to 2001/02, the proportion
of mathematics trainees with a 2:1 degree or better remained fairly constant
at below 40 per cent, varying between 33 and 38 per cent. |
| 2.57 |
Figure 2.14 presents comparative data for a range of subjects showing
the proportion of recruits to ITT with a degree class of 2:1 or better over
the period 1996/97 to 2001/02. The proportions are calculated as a percentage
of all first year trainees, including trainees who do not have a UK degree
and for whom degree classification is unknown. For modern foreign languages
(MFL), the proportion of trainees with non-UK degrees is higher and this
goes some way to explain the lower percentage of trainees with a 2:1 or higher
in this category. However, we are not aware of a similar mitigating factor
for mathematics. We therefore note, with considerable concern, that the
proportion of entrants with a 2:1 or higher entrants for mathematics teacher
training is the lowest of all the subjects. |
|
 |
| 2.58 |
This clearly suggests that teaching is not as attractive to the pool
of students who could teach mathematics as it is for potential teachers of
many other subjects and that, among entrants to the teaching profession,
subject-specific competence may not be so high in mathematics as in many
other subjects. This suggests that, in general, many teachers of mathematics
may be in more need of subject-specific CPD than teachers in other subjects.
We shall return to this issue in Chapters 5 and 6. |
| |
|
Returners to the profession
|
| 2.59 |
SET for Success drew attention to the small but growing number
of returners to the science teaching profession, as well as the increase
in mature entrants to the profession. Given the relatively small number of
graduates in mathematics, late entrants to the teaching profession in these
subjects are likely to become increasingly important and the Inquiry was
interested to learn of the Government’s “Welcome back bonus”
scheme for teachers returning to the profession that existed between Easter
and Christmas 2001. Teachers returning in a shortage subject such as mathematics
received £1,000 shortly after returning, plus £3,000 around a year
later. We understand that there are currently no plans to reintroduce this
scheme, but would wish to encourage this to be reconsidered. |
| |
|
Advanced Skills Teachers and Fast Track Schemes
|
| 2.60 |
The Advanced Skills Teacher (AST) grade was introduced in 1998 and offers
a new career route with an enhanced salary scale for excellent teachers who
do not wish to take up management posts. ASTs continue to work mainly as
classroom teachers but also spend time working with teachers in their own
and other schools to raise teaching and learning standards. To qualify for
an AST post teachers have to pass a rigorous assessment process. Schools
receive a grant jointly funded by the DfES and the Local Education Authority
to cover the additional cost of creating an AST post. The Inquiry believes
that a substantial increase in the number of mathematics ASTs is required,
not least to lead on the CPD agenda which we discuss in detail in Chapters
5 and 6 (see Recommendation 2.4 below). |
| 2.61 |
The DfES has introduced a Fast Track Scheme aimed at improving career
progression for individuals with the greatest leadership potential. It aims
to identify and develop those teachers who will eventually become an AST,
or part of the senior management team of a school. A total of 340 people
joined the programme in September 2003 either as trainees or existing teachers
and it is planned that numbers will continue to grow to several hundred a
year. The long-term aim is for 5 per cent of the teaching profession to be
on (or to have been through) the Fast Track programme. Teachers on the Fast
Track receive enhanced salaries. New entrants to the programme who come through
Fast Track initial teacher training receive an additional spine point on
the Main Pay Scale and a £5,000 bursary. All Fast Track teachers receive
a Recruitment and Retention allowance (about £2,000) once they have
completed their induction year in a maintained school. |
| 2.62 |
There is a separate fast track scheme for London. Teach First is a general
initiative to attract high quality graduates to teach in London. Teach First
has attracted investment by industry and commerce and in its first year has
attracted a relatively high proportion of mathematics graduates. The Inquiry
encourages the TTA and the DfES to monitor and evaluate this and similar
schemes and to be prepared, if appropriate, to provide resources to help
expand and sustain such initiatives. We would also encourage the LSC to work
with the DfES and TTA on these and other issues relating to teacher recruitment
(see, also, Recommendation 2.1). |
|
Recommendation 2.4
The Inquiry recommends that the DfES give high priority to encouraging and
funding a significant increase in the number of mathematics graduates admitted
to the Fast Track Scheme and, in particular, a significant increase in the
number of mathematics ASTs. |
| |
|
Incentives and the rise in PGCE applications in mathematics
|
| 2.63 |
Respondents to the Inquiry have expressed the view that Golden Hellos
and the introduction of the training bursaries in September 2000 have had
a significant effect on PGCE applications. Cumulative applications for
mathematics PGCE course are shown below in Figure 2.15. |
|
 |
| 2.64 |
The Inquiry welcomes these incentives and believes they are likely to
have contributed to the increased number of people on initial teacher training
courses. However, the financial inducements have now remained at the same
monetary level for three years and need reviewing. We believe it to be important
to ensure that the real level of these incentives is at least maintained. |
| |
|
The need to look beyond the pool of mathematics graduates
|
| 2.65 |
The Inquiry has noted with concern the data in Table 2.12 showing that
it would require 40 per cent of the current output of UK mathematics graduates
to fill all the allocated ITT training places in mathematics. With 2,350
allocated places for mathematics for 2004/05 the pressure to recruit mathematics
graduates is significantly greater than in 2000. |
|
Table 2.12: Percentage of mathematics graduates needed to fill allocated
mathematics ITT places
|
| Academic year |
Number of graduates |
Number of allocated places |
per cent of graduates required to meet allocation |
| 2002/03 |
3,380 |
1,759 |
52 |
| 2001/02 |
3,375 |
1,075 |
52 |
| 2000/01 |
4,235 |
1,876 |
44 |
| 1999/00 |
4,060 |
1,710 |
42 |
| 1998/99 |
4,214 |
2,126 |
50 |
| Source: TTA |
|
| 2.66 |
It is clear to the Inquiry that the supply of mathematics graduates applying
for ITT will be insufficient to meet the demand for trainee teachers for
many years to come. It is important therefore that the TTA and ITT providers
work together to try to identify and attract a wider pool of people to recruit
from. This includes finding ways of enabling people from a wider degree base
to train as teachers of mathematics. Suppose we assume that 40 per cent of
students achieving an A-level mathematics pass progress to higher education.
Even with the current drop to around 55,000 entries, which is likely to translate
to around 40,000 passes, this would imply a future population of close to
16,000 graduates per year (in practice, the percentage progressing to higher
education may be even higher than this figure) each with at least an A-level
in mathematics. Around 4000 obtain mathematics degrees. There is therefore
a potential pool of around 12,000 without a mathematics degree, but with
an A-level in mathematics. These include many graduates who may be capable
of enhancing their mathematics knowledge to allow them to teach to at least
Key Stage 3. At present, those in this group could gain access to courses
leading to primary teacher training, but would be unlikely to be able to
join a secondary PGCE course in mathematics (see Table 2.1). |
| 2.67 |
Where a trainee’s previous degree does not cover the spectrum of
knowledge required to teach a particular subject, pre- and in-course study
courses and subject support courses are available with access to help from
specialist tutors. These are currently being evaluated to assess their impact.
Some providers offer two-year PGCE courses that provide more time for trainees
to develop their subject knowledge. The TTA also has plans to pilot a Pre-Initial
Teacher Training Mathematics Enhancement Course from January 2004. This
initiative will target graduates from a wider range of non-mathematics degree
backgrounds, to develop their knowledge and deepen their understanding of
mathematics prior to a PGCE or GTP course. From January 2004, the course
will be piloted in two regions each year, for two consecutive years. Each
course will have 20 allocated places. A working group of ITT providers,
undergraduate course tutors and schoolteachers has developed the course
specification for mathematics. Contracts will be awarded to provide enhancement
courses as a service to all providers of graduate routes to QTS within the
region. Course participants will receive a bursary of £150 a week for
the twenty-six weeks of the course. On successful completion of the course
participants will progress to available QTS bearing courses of their choice
within the region. |
| 2.68 |
These enhancement courses will be evaluated fully to identify action
for DfES, TTA, enhancement course providers and ITT providers and to inform
any ministerial decisions about national availability of enhancement courses.
The Inquiry believes that the enhancement routes being piloted by the TTA
may be of considerable importance in identifying new sources of students
for recruitment into mathematics teacher training. This prompts the following
recommendation, which we would like to see also taken into account by those
responsible for the supply of mathematics teachers in colleges. |
| |
|
More specific certification of mathematics teachers
|
|
Recommendation 2.5
The Inquiry recommends that the current TTA enhancement programmes for graduates
be evaluated carefully and that additional resources be made available to
support and reinforce successful programmes in mathematics. The Inquiry further
recommends that the TTA should consider introducing enhancement programmes
that offer non-graduate career changers opportunities, including bursaries,
to complete graduate mathematics course and secure QTS. The Inquiry recommends
that, subject to appropriate quality assurance, the DfES give high priority
to providing any extra resources required by the TTA in expanding mathematics
enhancement programmes. |
| 2.69 |
In considering the need to provide enhancement to attract non-mathematics
graduates into mathematics teacher training, the Inquiry has been led to
consider whether there should just be a single certification scheme for QTS,
as at present, or whether instead there should be new routes which make it
possible to gain specific certification to teach mathematics up to specific
levels; for example, KS3, KS4 and post–16 levels. We believe this could
be extremely helpful in ensuring the supply of sufficient numbers of mathematics
teachers across all stages of learning and we therefore make the following
recommendation. |
|
Recommendation 2.6
The Inquiry recommends that consideration be given to the introduction of
new mathematics teacher certification schemes, aimed at increasing the overall
supply of teachers appropriately qualified to teach at least some part of
the curriculum. |
| |
|
Career Exploration
|
| 2.70 |
The TTA operates a range of programmes to enable prospective applicants
to become more informed about teaching and training to teach:
-
The Open Schools programme provides opportunities for people at an early
stage of exploring teaching as a career to spend an observation day in school;
-
The Teaching Advocates programme harnesses the enthusiasm of serving teachers
to support the TTA in various recruitment activities;
-
The Taster Courses programme aims to provide an in-depth taste of teaching
and teacher training. The courses last three days and include one full day
in school.
|
| 2.71 |
The Inquiry welcomes the fact that the TTA is now working to ensure that
the provision of these services is focussed on the need to improve recruitment
to priority subjects. Approximately 10 per cent of those making use of the
programmes are people interested in teaching secondary mathematics. Another
scheme managed by the TTA is the Student Associates Scheme. This is designed
for undergraduates currently uncommitted to a teaching career to enable them
to explore the possibility of teaching and give them a taste of life in school.
Universities pay a small bursary to the undergraduates for the time they
spend in schools. The second stage of the Scheme is only open to those who
have the qualifications required for entry into ITT and 40 per cent of the
Scheme is targeted at students from secondary shortage areas. It is anticipated
that 5,000 undergraduates will participate in the Scheme in the academic
year 2003/04. The scheme allows them to build up a portfolio of evidence
towards the standards for QTS, with a view to having that evidence taken
into account either in relation to the overall time spent on a PGCE course,
or in relation to the work required on specific parts of the course. |
| 2.72 |
Evaluation of the Scheme so far and of the experiences of a sample of
60 students from the academic year 2001/02 has been undertaken. Student reaction
to the Scheme has been very positive overall. There is also evidence from
training providers that students who had experience of the scheme were better
prepared for the PGCE interview process and more confident and better prepared
for their first teaching placement. The Inquiry welcomes the introduction
of this Scheme and is pleased to note that it has recently been expanded
to 5,000 places a year. However, we would like to see more targeted use of
the Scheme for mathematics students. |
|
Recommendation 2.7
The Inquiry recommends that a significant number of places in the Student
Associate Scheme be earmarked for undergraduates on degree courses in mathematics
or courses involving a substantial component of mathematics. We encourage
the TTA to work closely with the Committee of the Heads of Departments of
Mathematical Sciences (HoDMS) and others in higher education to continue
to raise the level of awareness of the scheme among relevant undergraduates. |
| 2.73 |
TTA Student Associate Scheme also supports the Undergraduate Ambassadors
Scheme pioneered by the writer and broadcaster, Simon Singh. The scheme operates
across all science, technology and engineering areas, as well as mathematics.
This is a further possible route to encouraging students into teaching, as
well as providing additional teaching resource in schools. The scheme operates
through higher education departments creating an undergraduate module in
which undergraduates acquire academic credit for time spent in schools and
for acquiring transferable skills in the context of their work in the classroom.
There are no financial payments. The scheme began in 2002 with a total of
twenty-eight students; this increased to around one hundred students in 2003
and four hundred in 2004. We provide further discussion of this and possible
related schemes in paragraphs 6.19-21 and in Recommendations 6.3 and 6.4. |
| |
|
|
|
| 2.74 |
From 1 September 2002, teachers in maintained secondary schools have
been paid on a new six-point salary scale. Once at the top of the scale,
they may apply to “cross the threshold” and move to a higher,
performance-related pay scale. One of five management allowances may be awarded
in addition to pay scale points to teachers on either of these scales, for
example to heads of department and other teachers with significant specialised
management responsibilities. In addition, any teacher may apply to become
an Advanced Skills Teacher and, if successful, will move to a new higher
pay scale. |
| 2.75 |
Schools in theory have considerable freedom over the pay of their teachers.
Schools are also able to use recruitment and retention allowances to attract
and keep key members of staff. At present, DfES evidence to the Inquiry suggests
that around 3 per cent of all teachers receive such an allowance. In relation
to the use of this flexibility for teachers of mathematics, the 2001/02 Annual
Report of Her Majesty’s Chief Inspector of Schools notes that
“Despite the flexibility that schools have to award recruitment and
retention allowances to attract high-quality teachers, many, particularly
in the primary sector, are reluctant to use them as they regard them as divisive
and unfair to existing staff. In secondary schools, use of recruitment and/or
incentive allowances to attract and retain staff, especially subject specialists
in mathematics and science is, however, increasing.”
|
| 2.76 |
SET for Success regarded the issue of teachers’ remuneration
as critically important and recommended that more needs to be done to address
pay and other incentives offered to teachers in shortage subjects. The Inquiry
strongly endorses this view. There is a shortage of mathematically qualified
graduates and schools and colleges are competing with other sectors of the
economy. We therefore echo the recommendation made in SET for Success. |
|
Recommendation 2.8
The Inquiry recommends that more must be done to address the issue of pay
and other incentives to teachers of mathematics and other shortage subjects
(see, also, Recommendation 5.2). |
| 2.77 |
The Government has recently introduced a pilot scheme (from 2002/03 for
three years) under which teachers in shortage subjects will also benefit
from having their student loans written-off for them over a period of time.
Current proposals would further increase the effective salaries of mathematics
teachers, potentially by up to around £1,500 per year for the first
ten years. The Inquiry welcomes this further attempt to provide incentives
for the recruitment of mathematics teachers. However, we are concerned at
the rather hit-and-miss and potentially unfair nature of the incentive, which
clearly has no impact on students who, for whatever reason, did not take
out loans (including those who may, at some personal cost, have worked to
support themselves through university). More fundamentally, we note that
the Government’s current HE Bill, which received its second reading
on 4 February 2004, proposes radical changes to future fee levels in higher
education. The Inquiry believes that the proposed fee changes open up important
new opportunities for substantial incentives through fee waivers and loan
write-offs. The Inquiry urges the Government to consider how to exploit these
opportunities to encourage teacher recruitment in shortage subjects. |
| |
|
|
|
|
Wales
|
| 2.78 |
The 2002 General Teaching Council for Wales (GTCW) survey of teacher
recruitment indicated that secondary mathematics posts attract significantly
fewer applicants than other subjects. In addition the number of applicants
per mathematics post is declining. In Welsh medium schools the situation
is worse. Recruitment is likely to be affected by the limited pool of Welsh
speaking teachers available. Mathematics and English are the posts most difficult
to fill in Welsh secondary maintained schools, despite a low overall teacher
vacancy rate of 0.4 per cent. Over ten per cent of mathematics teachers at
key stage 4 and above do not have a degree in mathematics or a closely related
subject. |
| 2.79 |
However, there are a number of incentives being provided to both postgraduate
and undergraduate trainee teachers. Encouragingly, the number of graduates
accepted onto PGCE ITT mathematics courses in Wales has risen by 15 per cent
in 2002–03, with a further increase in applicants for courses starting
in September 2003. |
|
Northern Ireland
|
| 2.80 |
Responses to the Inquiry from Northern Ireland have expressed the view
that mathematics teachers in Northern Ireland are more likely to be qualified
mathematicians than their colleagues in England. However, respondents felt
that there is a need to ensure the effective professional development of
mathematics specialists (see Chapters 5 and 6). |
| 2.81 |
A recent recruitment survey of all Northern Ireland post-primary schools
was conducted by some of Northern Ireland’s Education and Library Board
Officers. There was a high response rate of around 89 per cent. So far as
full-time posts were concerned, Grammar schools indicated that mathematics
is for the most part taught by teachers with appropriate training. Posts
are filled on time and without additional inducements. However, around 45
per cent had experienced some form of difficulty with recruitment. Grammar
schools also highlighted a lack of teachers qualified to cover Additional
Mathematics, AS and A2. Integrated schools met more problems in recruiting
full-time mathematics teachers and enhancements were typically used when
recruiting Heads of Department. Non-grammar schools found it the most difficult
to recruit appropriately qualified mathematics specialists. As a result,
schools often have to appoint under-qualified teachers and despite this some
posts need to be re-advertised. Enhancements are used both to recruit and
to retain teachers. This lack of teachers and appropriate skills are felt
to have a negative impact on students. In terms of substitute teacher
recruitment, most schools had experienced difficulties. Substitute teachers
prove even harder, if not impossible to recruit. Although some schools are
able to call on retired teachers for additional cover, there is a concern
that this may result in out of date teaching. In outlying areas, such teachers
are often simply not available. |
|
Scotland
|
| 2.82 |
In Scotland, since 2000/01 mathematics teachers have been required to
have studied the subject for three years at university. Responses to the
Inquiry indicate that although there is no overall shortage of teachers in
Scotland, mathematics is among the secondary school subjects in which it
is hardest to fill vacancies. The Scottish Executive has developed a three-tier
prioritisation system to ensure an adequate supply in all subjects: mathematics
is in the first category. However, overall, in November 2003 only 35 posts
in mathematics (2 per cent) were vacant and only 10 of those had been vacant
for more than three months. |
| 2.83 |
The teaching workforce in Scotland is ageing, which necessitates an ongoing
annual increase in the number of new teachers. This may become a problem.
Currently, there are no major shortages, however mathematics is one of the
more difficult areas. Scotland is currently among the handful of European
countries with a reasonable equilibrium between teacher supply and demand.
According to the Scottish Executive national statistics publication Results
of Teacher Workforce Planning for 2003–2004, five per cent of the
overall workforce joined or re-joined the workforce during 2000–2001,
and five per cent left during this time. |
| 2.84 |
It is the responsibility of Education Authorities and head teachers to
deploy staff as effectively as possible to meet local needs. Scotland currently
has no plans to make use of HE resources, such as using students as teaching
assistants. |














